
【题目】如图(1)五边形![]() 中,
中, ![]()
![]() ,将
,将![]() 沿
沿![]() 折到
折到![]() 的位置,得到四棱锥
的位置,得到四棱锥![]() ,如图(2),点
,如图(2),点![]() 为线段
为线段![]() 的中点,且
的中点,且![]() 平面
平面![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 与所成角的正切值为
与所成角的正切值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
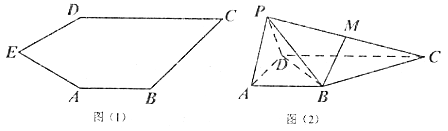
【答案】(1)见解析(2)![]()
【解析】试题分析: (1)根据已知条件由线线垂直得出线面垂直,再根据面面垂直的判定定理证得成立; (2)通过已知条件求出各边长度,建系如图所示,求出平面![]() 的法向量,根据线面角公式代入坐标求得结果.
的法向量,根据线面角公式代入坐标求得结果.
试题解析:(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,
,
又![]() ,所以
,所以![]() ,则四边形
,则四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,
,
又![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() .
.
由![]() 即
即![]() 及
及![]() 为
为![]() 的中点,可得
的中点,可得![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
又![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() 平面
平面![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(2)解:
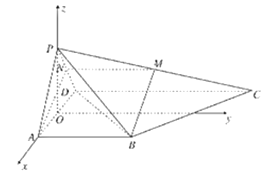
![]() ,∴
,∴![]() 为直线
为直线![]() 与
与![]() 所成的角,
所成的角,
由(1)可得![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
设![]() ,则
,则![]() ,
,
取![]() 的中点
的中点![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() 的平行线,
的平行线,
可建立如图所示的空间直角坐标系![]() ,
,
则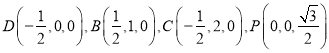 ,
,
∴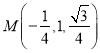 ,
,
所以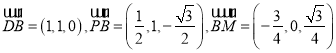 ,
,
设![]() 为平面
为平面![]() 的法向量,则
的法向量,则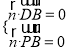 ,即
,即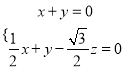 ,
,
取![]() ,则
,则![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
∵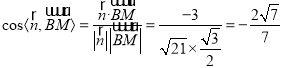 ,
,
则直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
点睛: 判定直线和平面垂直的方法:①定义法.②利用判定定理:一条直线和一个平面内的两条相交直线都垂直,则该直线和此平面垂直.③推论:如果在两条平行直线中,有一条垂直于一个平面,那么另一条直线也垂直于这个平面.平面与平面垂直的判定方法:①定义法.②利用判定定理:一个平面过另一个平面的一条垂线,则这两个平面垂直.


科目:高中数学 来源: 题型:
【题目】《九章算术》中有这样一则问题:“今有良马与弩马发长安,至齐,齐去长安三千里,良马初日行一百九十三里,日增一十三里;弩马初日行九十七里,日减半里,良马先至齐,复还迎弩马.”则现有如下说法:
①弩马第九日走了九十三里路;
②良马前五日共走了一千零九十五里路;
③良马和弩马相遇时,良马走了二十一日.
则以上说法错误的个数是( )个
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,且f(x)在(﹣∞,0]上单调递减,则不等式f(lgx)>f(﹣2)的解集是( )
A.( ![]() ,100)
,100)
B.(100,+∞)
C.( ![]() ,+∞)
,+∞)
D.(0, ![]() )∪(100,+∞)
)∪(100,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体P﹣ABCD中,平面ABCD⊥平面PAB,四边形ABCD为矩形,△PAB为正三角形,若AB=2,AD=1,E,F 分别为AC,BP中点. 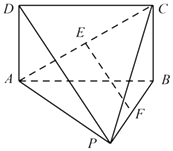
(Ⅰ)求证EF∥平面PCD;
(Ⅱ)求直线DP与平面ABCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品数,其中![]() 表示每件药材的重量,则图中①,②两处依次应该填的整数分别是____________.
表示每件药材的重量,则图中①,②两处依次应该填的整数分别是____________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为[﹣1,2],则函数g(x)=f(2x﹣ ![]() )的定义域为( )
)的定义域为( )
A.[ ![]() ,
, ![]() ]
]
B.[1, ![]() ]
]
C.[﹣1, ![]() ]
]
D.[﹣1, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某青少年成长关爱机构为了调研所在地区青少年的年龄与身高壮况,随机抽取6岁,9岁,12岁,15岁,18岁的青少年身高数据各1000个,根据各年龄段平均身高作出如图所示的散点图和回归直线![]() .根据图中数据,下列对该样本描述错误的是( )
.根据图中数据,下列对该样本描述错误的是( )
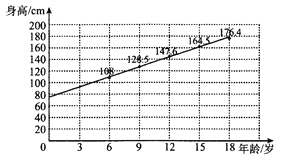
A. 据样本数据估计,该地区青少年身高与年龄成正相关
B. 所抽取数据中,5000名青少年平均身高约为![]()
C. 直线![]() 的斜率的值近似等于样本中青少年平均身高每年的增量
的斜率的值近似等于样本中青少年平均身高每年的增量
D. 从这5种年龄的青少年中各取一人的身高数据,由这5人的平均年龄和平均身高数据作出的点一定在直线![]() 上
上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,E,F,G分别为A1B1 , BB1 , B1C1的中点,则AC1与D1E所成角的余弦值为 , AC1与平面EFG所成角的正弦值为 . 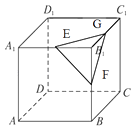
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com