Question

【题目】如图，已知OPQ是半径为 圆心角为 的扇形，C是该扇形弧上的动点，ABCD是扇形的内接矩形，记∠BOC为α．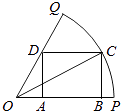
（Ⅰ）若Rt△CBO的周长为 ，求 的值．
（Ⅱ）求 的最大值，并求此时α的值．

Answer 1

【答案】解：（Ⅰ）BC=OCsinα= sinα，OB=OCcosα= cosα，

则若Rt△CBO的周长为 ，

则 + sinα+ cosα= ，

sinα+cosα= ，

平方得2sinαcosα= ，

即 = = ，

解得tanα=3（舍）或tanα= ．

则 = = = = ．

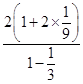（Ⅱ）在Rt△OBC中，BC=OCsinα= sinα，OB=OCcosα= cosα，

在Rt△ODA中，

OA=DAtan = BC= sinα，

∴AB=OB﹣OA= （cosα﹣ cosα），

则 =| | |= （cosα﹣ cosα） sinα

=

∵ ，

∴ ，

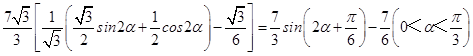
∴当 ，

即 时， 有最大值 ．

【解析】（Ⅰ）由条件利用直角三角形中的边角关系求出三角形的周长，利用三角函数的倍角公式进行化简进行求解．（Ⅱ）结合向量的数量积公式，结合三角函数的带动下进行求解．
【考点精析】本题主要考查了扇形面积公式的相关知识点，需要掌握若扇形的圆心角为，半径为，弧长为，周长为，面积为，则，，才能正确解答此题．