
【题目】设两个非零向量 ![]() 与
与 ![]() 不共线.
不共线.
(1)若 ![]() =
= ![]() +
+ ![]() ,
, ![]() =2
=2 ![]() +8
+8 ![]() ,
, ![]() =3(
=3( ![]() ﹣
﹣ ![]() ).求证:A,B,D三点共线;
).求证:A,B,D三点共线;
(2)试确定实数k,使k ![]() +
+ ![]() 和
和 ![]() +k
+k ![]() 共线.
共线.
【答案】
(1)解:∵ ![]() =
= ![]()
= ![]() =
= ![]() ,
,
∴ ![]() 与
与 ![]() 共线
共线
两个向量有公共点B,
∴A,B,D三点共线.
(2)解:∵ ![]() 和
和 ![]() 共线,则存在实数λ,使得
共线,则存在实数λ,使得 ![]() =λ(
=λ( ![]() ),
),
即 ![]() ,
,
∵非零向量 ![]() 与
与 ![]() 不共线,
不共线,
∴k﹣λ=0且1﹣λk=0,
∴k=±1.
【解析】(1)根据所给的三个首尾相连的向量,用其中两个相加,得到两个首尾相连的向量,根据表示这两个向量的基底,得到两个向量之间的共线关系,从而得到三点共线.(2)两个向量共线,写出向量共线的充要条件,进而得到关于实数k的等式,解出k的值,有两个结果,这两个结果都合题意.
【考点精析】本题主要考查了向量的共线定理的相关知识点,需要掌握设![]() ,
,![]() ,其中
,其中![]() ,则当且仅当
,则当且仅当![]() 时,向量
时,向量![]() 、
、![]() 共线才能正确解答此题.
共线才能正确解答此题.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆方程为 ![]() =1(a>0,b>0),其右焦点为F(4,0),过点F的直线交椭圆与A,B两点.若AB的中点坐标为(1,﹣1),则椭圆的方程为( )
=1(a>0,b>0),其右焦点为F(4,0),过点F的直线交椭圆与A,B两点.若AB的中点坐标为(1,﹣1),则椭圆的方程为( )
A.![]() =1
=1
B.![]() =1
=1
C.![]() +
+ ![]() =1
=1
D.![]() =1
=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p: ![]() <1,q:x2+(a﹣1)x﹣a>0,若p是q的充分不必要条件,则实数a的取值范围是( )
<1,q:x2+(a﹣1)x﹣a>0,若p是q的充分不必要条件,则实数a的取值范围是( )
A.(﹣2,﹣1]
B.[﹣2,﹣1]
C.[﹣3,﹣1]
D.[﹣2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p: ![]() <1,q:x2+(a﹣1)x﹣a>0,若p是q的充分不必要条件,则实数a的取值范围是( )
<1,q:x2+(a﹣1)x﹣a>0,若p是q的充分不必要条件,则实数a的取值范围是( )
A.(﹣2,﹣1]
B.[﹣2,﹣1]
C.[﹣3,﹣1]
D.[﹣2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题中,其中正确的个数为( ) ①命题“若x2﹣3x+2=0,则x=1”的逆否命题为“若x≠1,则x2﹣3x+2=0”;
②“ ![]() ”是“cos2α=0”的充分不必要条件;
”是“cos2α=0”的充分不必要条件;
③若命题 ![]() ,则p:x∈R,x2+x+1=0;
,则p:x∈R,x2+x+1=0;
④若p∧q为假,p∨q为真,则p,q有且仅有一个是真命题.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知OPQ是半径为 ![]() 圆心角为
圆心角为 ![]() 的扇形,C是该扇形弧上的动点,ABCD是扇形的内接矩形,记∠BOC为α.
的扇形,C是该扇形弧上的动点,ABCD是扇形的内接矩形,记∠BOC为α. 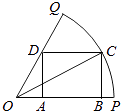
(Ⅰ)若Rt△CBO的周长为 ![]() ,求
,求 ![]() 的值.
的值.
(Ⅱ)求 ![]() 的最大值,并求此时α的值.
的最大值,并求此时α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为4,P为BC的中点,Q为线段CC1上的动点(异于C点),过点A,P,Q的平面截面记为M.
则当CQ∈时(用区间或集合表示),M为四边形;
当CQ=时(用数值表示),M为等腰梯形;
当CQ=4时,M的面积为 . 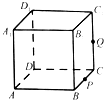
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点A(x,y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间t=0时,点A的坐标是 ![]() ,则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是( )
,则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是( )
A.[0,1]
B.[1,7]
C.[7,12]
D.[0,1]和[7,12]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com