练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】动点A（x，y）在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转，12秒旋转一周．已知时间t=0时，点A的坐标是 ，则当0≤t≤12时，动点A的纵坐标y关于t（单位：秒）的函数的单调递增区间是（ ）
    A.[0，1]
    B.[1，7]
    C.[7，12]
    D.[0，1]和[7，12]

    【答案】D
    【解析】解：设动点A与x轴正方向夹角为α，则t=0时 ，每秒钟旋转 ，在t∈[0，1]上 ，在[7，12]上 ，动点A的纵坐标y关于t都是单调递增的．

    所以答案是：D．

    【考点精析】通过灵活运用函数单调性的判断方法，掌握单调性的判定法：①设x1,x2是所研究区间内任两个自变量，且x1＜x2；②判定f(x1)与f(x2)的大小；③作差比较或作商比较即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设两个非零向量 与 不共线．
    （1）若 = + ， =2 +8 ， =3（ ﹣ ）．求证：A，B，D三点共线；
    （2）试确定实数k，使k + 和 +k 共线．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题中错误的个数为：（ ）
    ①y= 的图象关于（0，0）对称；
    ②y=x3+x+1的图象关于（0，1）对称；
    ③y= 的图象关于直线x=0对称；
    ④y=sinx+cosx的图象关于直线x= 对称．
    A.0
    B.1
    C.2
    D.3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    (1)求时，求的单调区间；

    (2)讨论在定义域上的零点个数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=2cosx（sinx+cosx），x∈R．
    （Ⅰ）求函数f（x）的最小正周期；
    （Ⅱ）求函数f（x）的单调递增区间；
    （Ⅲ）求函数f（x）在区间[﹣ ， ]上的最小值和最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知{an}是等差数列，满足a1=3，a4=12，数列{bn}满足b1=4，b4=20，且{bn﹣an}为等比数列．
    （1）求数列{an}和{bn}的通项公式；
    （2）求数列{bn}的前n项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆两焦点 ，并且经过点 ．
    （1）求椭圆的方程；
    （2）若过点A（0，2）的直线l与椭圆交于不同的两点M、N（M在A、N之间），试求△OAM与△OAN面积之比的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，角α（0≤α≤π）的始边为x轴的非负半轴，终边与单位圆的交点为A，将OA绕坐标原点逆时针旋转 至OB，过点B作x轴的垂线，垂足为Q．记线段BQ的长为y，则函数y=f（α）的图象大致是（ ）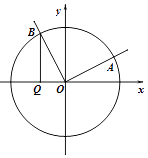

    A.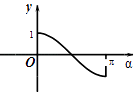
    B.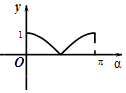
    C.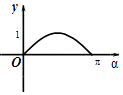
    D.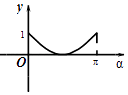

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知下列命题：（ ）
    ①向量 ， 不共线，则向量 与向量 一定不共线
    ②对任意向量 ， ，则 恒成立
    ③在同一平面内，对两两均不共线的向量 ， ， ，若给定单位向量 和正数 ，总存在单位向量 和实数 ，使得
    则正确的序号为（ ）
    A.①②③
    B.①③
    C.②③
    D.①②

    查看答案和解析>>

    同步练习册答案