
【题目】已知函数f(x)=2sin (2x+ ![]() ).
).
(1)求函数f(x)的最小正周期及其单调减区间;
(2)用“五点法”画出函数g(x)=f(x),x∈[﹣ ![]() ,
, ![]() ]的图象(完成列表格并作图),由图象研究并写出g(x)的对称轴和对称中心.
]的图象(完成列表格并作图),由图象研究并写出g(x)的对称轴和对称中心.
【答案】
(1)解:函数f(x)=2sin (2x+ ![]() ),
),
∴f(x)的最小正周期为T= ![]() =π;
=π;
令2kπ+ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,
,k∈Z,
则2kπ+ ![]() ≤2x≤2kπ+
≤2x≤2kπ+ ![]() ,k∈Z,
,k∈Z,
kπ+ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z;
,k∈Z;
∴函数f(x)的单调减区间为[kπ+ ![]() ,kπ+
,kπ+ ![]() ](k∈Z);
](k∈Z);
(2)解:根据题意列出表格得:
x | ﹣ | ﹣ | ﹣ |
|
|
2x+ | ﹣π | ﹣ | 0 |
| π |
y=2sin(2x+ | 0 | ﹣2 | 0 | 2 | 0 |
根据表格画出函数g(x)=f(x),x∈[﹣ ![]() ,
, ![]() ]的图象如图所示,
]的图象如图所示,
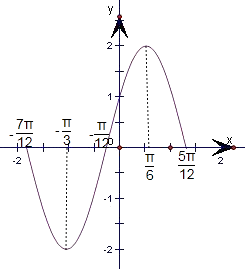
从图象上可以直观看出,此函数没有对称轴,有一个对称中心,对称中心是(﹣ ![]() ,0).
,0).
【解析】(1)根据正弦函数的图象与性质,求出f(x)的最小正周期与单调减区间;(2)根据题意列出表格,根据表格画出函数在x∈[﹣ ![]() ,
, ![]() ]的图象,结合图象得出此函数没有对称轴,有一个对称中心.
]的图象,结合图象得出此函数没有对称轴,有一个对称中心.
【考点精析】认真审题,首先需要了解五点法作函数y=Asin(ωx+φ)的图象(描点法及其特例—五点作图法(正、余弦曲线),三点二线作图法(正、余切曲线)).


科目:高中数学 来源: 题型:
【题目】某地区植被被破坏,土地沙化越来越严重,最近三年测得沙漠增加值分别为0.2万公顷、0.4万公顷、0.76万公顷,则沙漠增加数y(万公顷)关于年数x的函数关系较为近似的是( )
A.y=0.2x
B.![]()
C.![]()
D.y=0.2+log16x
查看答案和解析>>
科目:高中数学 来源: 题型:
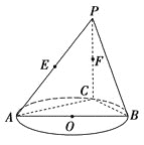
【题目】如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.
(1)记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明;
(2)设AB=PC=2,BC=1,求三棱锥P-BEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以
为参数),在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() ,与
,与![]() ,
, ![]() 各有一个交点,当
各有一个交点,当![]() 时,这两个交点间的距离为2,当
时,这两个交点间的距离为2,当![]() ,这两个交点重合.
,这两个交点重合.
(1)分别说明![]() ,
, ![]() 是什么曲线,并求出
是什么曲线,并求出![]() 与
与![]() 的值;
的值;
(2)设当![]() 时,
时, ![]() 与
与![]() ,
, ![]() 的交点分别为
的交点分别为![]() ,当
,当![]() ,
, ![]() 与
与![]() ,
, ![]() 的交点分别为
的交点分别为![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]()
(1)判断f(x)的奇偶性并证明;
(2)若f(x)的定义域为[α,β](β>α>0),判断f(x)在定义域上的增减性,并加以证明;
(3)若0<m<1,使f(x)的值域为[logmm(β﹣1),logmm(α﹣1)]的定义域区间[α,β](β>α>0)是否存在?若存在,求出[α,β],若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若a,b是函数f(x)=x2﹣px+q(p>0,q>0)的两个不同的零点,c<0且a,b,c这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则 ![]() ﹣2c的最小值等于( )
﹣2c的最小值等于( )
A.9
B.10
C.3
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某公司的职工食堂中,食堂每天以3元/个的价格从面包店购进面包,然后以5元/个的价格出售.如果当天卖不完,剩下的面包以1元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如图所示.食堂某天购进了 90个面包,以![]() (个)(其中
(个)(其中![]() )表示面包的需求量,
)表示面包的需求量, ![]() (元)表示利润.
(元)表示利润.
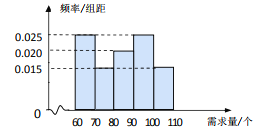
(1)根据直方图计算需求量的中位数;
(2)估计利润![]() 不少于100元的概率;
不少于100元的概率;
(3)在直方图的需求量分组中,以需求量落入该区间的频率作为需求量在该区间的概率,求![]() 的数学期望.
的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com