练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设a，b，c∈（﹣∞，0），则a+ ，b+ ，c+ （ ）
    A.都不大于﹣2
    B.都不小于﹣2
    C.至少有一个不大于﹣2
    D.至少有一个不小于﹣2

    【答案】C
    【解析】解：假设a+ ，b+ ，c+ 都大于﹣2， 即a+ ＞﹣2，b+ ＞﹣2，c+ ＞﹣2，
    将三式相加，得a+ +b+ +c+ ＞﹣6，
    又因为a，b，c∈（﹣∞，0），
    所以a+ ≤﹣2，b+ ≤﹣2，c+ ≤﹣2，
    三式相加，得a+ +b+ +c+ ≤﹣6，
    所以a+ +b+ +c+ ＞﹣6不成立．
    故选：C．
    【考点精析】本题主要考查了反证法与放缩法的相关知识点，需要掌握常见不等式的放缩方法：①舍去或加上一些项②将分子或分母放大（缩小)才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数在其定义域内有两个不同的极值点.

    （1）求的取值范围.

    （2）设的两个极值点为，证明

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ex
    （Ⅰ）求曲线f（x）过O（0，0）的切线l方程；
    （Ⅱ）求曲线f（x）与直线x=0，x=1及x轴所围图形的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，某城市有一块半径为40m的半圆形（以O为圆心，AB为直径）绿化区域，现计划对其进行改建．在AB的延长线上取点D，使OD＝80m，在半圆上选定一点C，改建后的绿化区域由扇形区域AOC和三角形区域COD组成，其面积为S m2. 设∠AOC＝x rad.

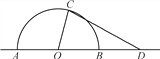
    （1）写出S关于x的函数关系式S(x)，并指出x的取值范围；

    （2）张强同学说：当∠AOC=时，改建后的绿化区域面积S最大．张强同学的说法正确吗？若不正确，请求出改建后的绿化区域面积S最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 .

    （Ⅰ）求曲线在点处的切线方程；

    （Ⅱ）求证： ；

    （Ⅲ）判断曲线是否位于轴下方，并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】过点（1，1）且与曲线y=x3相切的切线方程为（ ）
    A.y=3x﹣2
    B.y= x+
    C.y=3x﹣2或y= x+
    D.y=3x﹣2或y= x﹣

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】请您设计一个帐篷．它下部的形状是高为1m的正六棱柱，上部的形状是侧棱长为3m的正六棱锥（如图所示）．试问当帐篷的顶点O到底面中心O1的距离为多少时，帐篷的体积最大？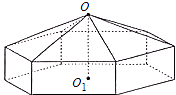

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=2sin （2x+ ）．
    （1）求函数f（x）的最小正周期及其单调减区间；
    （2）用“五点法”画出函数g（x）=f（x），x∈[﹣ ， ]的图象（完成列表格并作图），由图象研究并写出g（x）的对称轴和对称中心．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，函数.

    （1）当时，解不等式；

    （2）设，若对任意，函数在区间上的最大值与最小值的差不超过1，求的取值范围.

    查看答案和解析>>

    同步练习册答案