
����Ŀ����ͼ��ij������һ��뾶Ϊ40m�İ�Բ������OΪԲ�ģ�ABΪֱ�����̻������ּƻ�������иĽ�����AB���ӳ�����ȡ��D��ʹOD��80m���ڰ�Բ��ѡ��һ��C���Ľ�����̻���������������AOC������������COD��ɣ������ΪS m2. ���AOC��x rad.
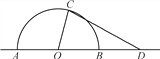
��1��д��S����x�ĺ�����ϵʽS(x)����ָ��x��ȡֵ��Χ��
��2����ǿͬѧ˵������AOC=![]() ʱ���Ľ�����̻��������S�����ǿͬѧ��˵����ȷ��������ȷ��������Ľ�����̻��������S���ֵ.
ʱ���Ľ�����̻��������S�����ǿͬѧ��˵����ȷ��������ȷ��������Ľ�����̻��������S���ֵ.
���𰸡���1��S��![]() ����2��
����2��![]()
�������������������1�������������AOC������������COD��������������S����x�ĺ�����ϵʽ![]() ����ָ��x��ȡֵ��Χ����2��������ȷ�������ĵ����ԣ����ɵó����ۣ�
����ָ��x��ȡֵ��Χ����2��������ȷ�������ĵ����ԣ����ɵó����ۣ�
���������
��1����Ϊ����AOC�İ뾶Ϊ40m����AOC��x rad��
��![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
����![]() ��
��
�Ӷ�![]()
![]() ��
��![]() ��
��
��2����ǿͬѧ��˵������ȷ.
�������£�
����1��֪�� ![]() .
.
![]() .
.
��![]() �����
�����![]() .
.
�Ӷ���![]() ʱ��
ʱ�� ![]() ����
����![]() ʱ��
ʱ�� ![]() .
.
���![]() ������
������![]() �ϵ���������������
�ϵ���������������![]() �ϵ����ݼ���
�ϵ����ݼ���
���Ե�![]() ʱ��Sȡ�����ֵ
ʱ��Sȡ�����ֵ![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�sin ![]() =
= ![]() ��AB=2����D���߶�AC�ϣ���AD=2DC��BD=
��AB=2����D���߶�AC�ϣ���AD=2DC��BD= ![]() ��������BC�ij����������DBC�������
��������BC�ij����������DBC������� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �ϵ�ż����
�ϵ�ż����![]() ����
����![]() ���ҵ�
���ҵ�![]() ʱ��
ʱ�� ![]() ������
������![]() �ڹ���
�ڹ���![]() �ķ���
�ķ���![]() ǡ��3����ͬ��ʵ��������
ǡ��3����ͬ��ʵ��������![]() ��ȡֵ��Χ�� �� ��
��ȡֵ��Χ�� �� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1��������![]() ������
������![]() �ϲ���������
�ϲ���������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
��2����![]() ���Ƿ����ʵ��
���Ƿ����ʵ��![]() ��������
��������![]() ������
������![]() ��ʹ��
��ʹ��![]() �����������ڣ���
�����������ڣ���![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �����г���
�������![]() .
.
��1����![]() ʱ������
ʱ������![]() �ĵ����������䣻
�ĵ����������䣻
��2����![]() ʱ��������
ʱ��������![]() ��������ͬ����㣬��
��������ͬ����㣬��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3���趨����![]() �ϵĺ���
�ϵĺ���![]() �ڵ�
�ڵ�![]() �������߷���Ϊ
�������߷���Ϊ![]() ����
����![]() ʱ����
ʱ����![]() ��
��![]() �ں���������
�ں���������![]() Ϊ����
Ϊ����![]() �ġ���ԳƵ㡱������̽����
�ġ���ԳƵ㡱������̽����![]() ʱ������
ʱ������![]() �Ƿ���ڡ���ԳƵ㡱�������ڣ����������һ������ԳƵ㡱 �ĺ����ꣻ�������ڣ�˵������.
�Ƿ���ڡ���ԳƵ㡱�������ڣ����������һ������ԳƵ㡱 �ĺ����ꣻ�������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
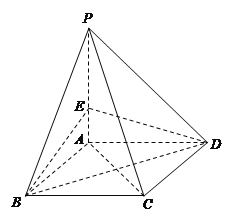
����Ŀ����ͼ��������![]() �У�����
�У�����![]() �����Σ�
�����Σ� ![]() ƽ��
ƽ��![]() ��
�� ![]() ����
����![]() �ϵ�һ�����㣮
�ϵ�һ�����㣮
������![]() Ϊ
Ϊ![]() ���е㣬��֤��
���е㣬��֤�� ![]() ƽ��
ƽ��![]() ��
��
��������֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
����������![]() �����������
�����������![]() �����
�����![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������б��Ϊ![]() �������ijλ��ʦ�Ӵ�����ȡ������ͬ����. ��ʦ����ȡ�����ŵĺ�ֻ���ף���˻�ֻ�����ң��üס��ҷֱ��ƶ���������ı��.
�������ijλ��ʦ�Ӵ�����ȡ������ͬ����. ��ʦ����ȡ�����ŵĺ�ֻ���ף���˻�ֻ�����ң��üס��ҷֱ��ƶ���������ı��.
��˵��������ȷ��.��
��˵������Ҳ��ȷ��.��
�������ҵĻش��Ժ���˵�����ҿ���ȷ����.��
����������Ϣ, ������ƶϳ���ȡ��������
A. һ����3���� B. һ��û��3���� C. ������5���� D. ������6����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij���豸ʹ�õ�����x���꣩����֧����ά����y��Ԫ��������ͳ�����ϣ�

�ο����ݣ� ![]() .�ο���ʽ:
.�ο���ʽ: ![]()

���������֪y��x��������ع�ϵ������
��1��![]() ��2�����Իع鷽��
��2�����Իع鷽��![]()
��3������ʹ��10��ʱ��ά�����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y=Asin����x+�գ���һ�������ڵ�ͼ����ͼ���˺����Ľ���ʽΪ�� �� 
A.y=2sin��2x+ ![]() ��
��
B.y=2sin��2x+ ![]() ��??
��??
C.y=2sin�� ![]() ��
�� ![]() ��
��
D.y=2sin��2x�� ![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com