
【题目】请您设计一个帐篷.它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心O1的距离为多少时,帐篷的体积最大? 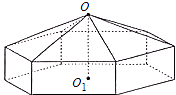
【答案】解:设OO1为xm,(1<x<4). 则由题设可得正六棱锥底面边长为: ![]() (m).
(m).
(求解过程为: ![]() )
)
于是底面正六边形的面积为(单位:m2) ![]()
帐篷的体积为(单位:m3) ![]() .
.
可得: ![]()
求导数,得 ![]()
令V'(x)=0解得x=﹣2(不合题意,舍去),x=2.
当1<x<2时,V'(x)>0,V(x)为增函数;
当2<x<4时,V'(x)<0,V(x)为减函数.
所以当x=2时,V(x)最大.
答当OO1为2m时,帐篷的体积最大.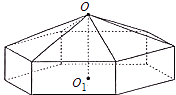
【解析】设出顶点O到底面中心o1的距离,再求底面边长和底面面积,求出体积表达式,利用导数求出高为何时体积取得最大值.
【考点精析】利用函数的最大(小)值与导数对题目进行判断即可得到答案,需要熟知求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为R,f(1)=3,对任意x∈R,f′(x)<2,则f(x)<2x+1的解集为( )
A.(1,+∞)
B.(﹣1,1)
C.(﹣∞,1)
D.(﹣∞,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)=x3﹣3x2 , 给出下列四个命题: ①f(x)是增函数,无极值;
②f(x)是减函数,有极值;
③f(x)在区间(﹣∞,0]及[2,+∞)上是增函数;
④f(x)有极大值为0,极小值﹣4;
其中正确命题的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区植被被破坏,土地沙化越来越严重,最近三年测得沙漠增加值分别为0.2万公顷、0.4万公顷、0.76万公顷,则沙漠增加数y(万公顷)关于年数x的函数关系较为近似的是( )
A.y=0.2x
B.![]()
C.![]()
D.y=0.2+log16x
查看答案和解析>>
科目:高中数学 来源: 题型:
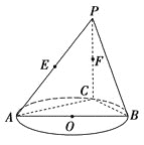
【题目】如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.
(1)记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明;
(2)设AB=PC=2,BC=1,求三棱锥P-BEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]()
(1)判断f(x)的奇偶性并证明;
(2)若f(x)的定义域为[α,β](β>α>0),判断f(x)在定义域上的增减性,并加以证明;
(3)若0<m<1,使f(x)的值域为[logmm(β﹣1),logmm(α﹣1)]的定义域区间[α,β](β>α>0)是否存在?若存在,求出[α,β],若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com