
已知椭圆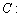
 (
(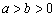 )的左,右焦点分别为
)的左,右焦点分别为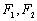 ,上顶点为
,上顶点为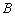 .
.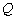 为抛物线
为抛物线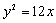 的焦点,且
的焦点,且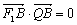 ,
,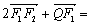 0.
0.
(Ⅰ)求椭圆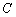 的标准方程;
的标准方程;
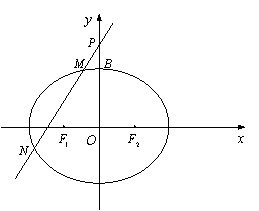
(Ⅱ)过定点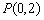 的直线
的直线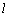 与椭圆
与椭圆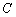 交于
交于 两点(
两点(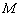 在
在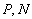 之间),设直线
之间),设直线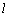
的斜率为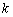 (
(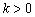 ),在
),在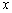 轴上是否存在点
轴上是否存在点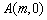 ,使得以
,使得以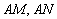 为邻边的平行四边形为菱形?若存在,求出实数
为邻边的平行四边形为菱形?若存在,求出实数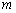 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
 |
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案科目:高中数学 来源: 题型:
定义集合运算:A·B={Z|Z=xy,x∈A,y∈B},设集合A={-1,0,1},B={sinα,cosα},则集合A·B的所有元素之和为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
给出下列四个命题:
①直线垂直于一个平面内的无数条直线是这条直线与这个平面垂直的充要条件;
②过空间一定点有且只有一条直线与已知平面垂直;
③不在一个平面内的一条直线和平面内的一条直线平行是这条直线和这个平面平行的充分条件;
④一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,则这两个二面角相等或互补.
其中真命题的为( )
A.①③ B.②④ C.②③ D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com