练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数 ，

    （1）求函数的最小正周期和单调递减区间；

    （2）当时，求的最大值和最小值．


    解 ：（Ⅰ）由题设得：f（x）=（sinx+cosx）2+2cos2x=1+sin2x+2cos2x

    =sin2x+cos2x+2=，  

    ∴f（x）的最小正周期为π， 分）

    令（k∈Z）得，≤x≤，k∈z

    ∴f（x）的单调递减区间为[，]（k∈Z）．-

    （Ⅱ）∵x∈[0，]，∴，

    ∴，

    ∴，

    ∴当x=时，f（x）取到最小值为1

    当x=时，f（x）取到最大值为2+．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    利用下列盈利表中的数据进行决策，应选择的方案是________．

    　　　                     方案

    盈利 　　

    概率　　　　　

    A1

    A2

    A3

    A4

    0.25

    50

    70

    －20

    98

    0.30

    65

    26

    52

    82

    0.45

    26

    16

    78

    －10

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某种产品的广告费支出x(单位：百万元)与销售额y(单位：百万元)之间有如下对应数据：

     

    x

    2

    4

    5

    6

    8

    y

    30

    40

    60

    50

    70

    (1)试根据表中数据估计广告费支出1 000万元时的销售额；

    (2)若广告费支出1 000万元时的实际销售额为8 500万元，求误差．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数的最小正周期是 (    )

    A.           B. 3              C.         D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在各项都为正项的等比数列{an}中a1 = 3, S 3 = 21 , 则a3+ a4+ a5 =               .

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知抛物线y2＝2px(p＞0)的准线与曲线x2＋y2－6x－7＝0相切，则p的值为(　　)

    A．2     B．1

    C.     D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在平面直角坐标系xOy中，直线l与抛物线y2＝4x相交于不同的A，B两点．

    (1)如果直线l过抛物线的焦点，求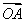·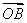的值；

    (2)如果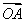·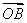＝－4，证明直线l必过一定点，并求出该定点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，平面内有三个向量、、,其中与的夹角为120°，与的夹角为30°,且||＝||＝1， || ＝，若则的值为       .

          

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数是周期为2的周期函数，且当时，，则函数的零点个数是

    A．9            B．10           C．11            D．18

    查看答案和解析>>

    同步练习册答案