
在平面直角坐标系xOy中,直线l与抛物线y2=4x相交于不同的A,B两点.
(1)如果直线l过抛物线的焦点,求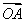 ·
·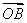 的值;
的值;
(2)如果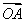 ·
·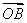 =-4,证明直线l必过一定点,并求出该定点.
=-4,证明直线l必过一定点,并求出该定点.
解:(1)由题意:抛物线焦点为(1,0),
设l:x=ty+1,代入抛物线y2=4x,
消去x得y2-4ty-4=0,
设A(x1,y1),B(x2,y2),则y1+y2=4t,
y1y2=-4,
∴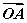 ·
·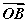 =x1x2+y1y2=(ty1+1)(ty2+1)+y1y2=t2y1y2+t(y1+y2)+1+y1y2
=x1x2+y1y2=(ty1+1)(ty2+1)+y1y2=t2y1y2+t(y1+y2)+1+y1y2
=-4t2+4t2+1-4=-3.
(2)证明:设l:x=ty+b代入抛物线y2=4x,消去x得
y2-4ty-4b=0,设A(x1,y1),B(x2,y2),
则y1+y2=4t,y1y2=-4b,
∴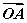 ·
·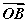 =x1x2+y1y2=(ty1+b)(ty2+b)+y1y2=t2y1y2+bt(y1+y2)+b2+y1y2
=x1x2+y1y2=(ty1+b)(ty2+b)+y1y2=t2y1y2+bt(y1+y2)+b2+y1y2
=-4bt2+4bt2+b2-4b=b2-4b.
令b2-4b=-4,∴b2-4b+4=0,∴b=2.
∴直线l过定点(2,0).
∴若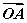 ·
·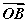 =-4,则直线l必过一定点(2,0).
=-4,则直线l必过一定点(2,0).


科目:高中数学 来源: 题型:
如图2,一个小球从M处投入,通过管道自上而下落到A或B或C.已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A、B、C,则分别设为1,2,3等奖.
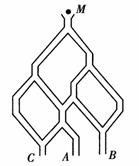
图2
(1)已知获得1,2,3等奖的折扣率分别为50%,70%,90%.记随变量ξ为获得k(k=1,2,3)等奖的折扣率.求随机变量ξ的概率分布及期望E(ξ);
(2)若有3人次(投入1球为1人次)参加促销活动,记随机变量η为获得1等奖或2等奖的人次,求P(η=2).
查看答案和解析>>
科目:高中数学 来源: 题型:
巴西医生马廷恩收集了犯有贪污、受贿罪官员的寿命与廉洁官员寿命的调查资料:500名贪官中有348人的寿命小于平均寿命,152人的寿命大于或等于平均寿命;580名廉洁官中有93人的寿命小于平均寿命,487人的寿命大于或等于平均寿命.这里,平均寿命是指“当地人均寿命”.试分析官员在经济上是否清白与他们寿命的长短是否有关.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知抛物线y2=2px的焦点F与双曲线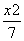 -
-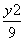 =1的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上,且|AK|=
=1的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上,且|AK|=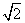 |AF|,则△AFK的面积为( )
|AF|,则△AFK的面积为( )
A.4 B.8
C.16 D.32
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com