练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图2，一个小球从M处投入，通过管道自上而下落到A或B或C.已知小球从每个叉口落入左右两个管道的可能性是相等的．某商家按上述投球方式进行促销活动，若投入的小球落到A、B、C，则分别设为1，2，3等奖．

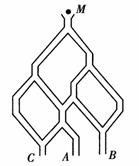
    图2

    (1)已知获得1，2，3等奖的折扣率分别为50%，70%，90%.记随变量ξ为获得k(k＝1，2，3)等奖的折扣率．求随机变量ξ的概率分布及期望E(ξ)；

    (2)若有3人次(投入1球为1人次)参加促销活动，记随机变量η为获得1等奖或2等奖的人次，求P(η＝2)．


    【解】　(1)由题意，得ξ的概率分布为：

     

    ξ

    50%

    70%

    90%

    P

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    回归直线方程为y=0.5x0.81，则x=25时，y的估计值为               .

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用反证法证明命题：“若x，y > 0，且x + y > 2，则，中至少有一个小于2”时，假设的内容应为                            ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    利用下列盈利表中的数据进行决策，应选择的方案是________．

    　　　                     方案

    盈利 　　

    概率　　　　　

    A1

    A2

    A3

    A4

    0.25

    50

    70

    －20

    98

    0.30

    65

    26

    52

    82

    0.45

    26

    16

    78

    －10

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    甲、乙两人独立解某一道数学题，已知甲独立解出的概率为0.6，且两人中至少有一人解出的概率为0.92.   

    (1)求该题被乙独立解出的概率；

    (2)求解出该题的人数X的概率分布．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    为了研究两个变量x和y之间的线性相关性，甲、乙两位同学各自独立地做了10次和15次试验，并且利用线性回归方程，求得回归直线分别为l1和l2.已知两个人在试验中发现对变量x的观测数据的平均值都为s，对变量y的观测数据的平均值都为t，那么下列说法正确的是   ________．

    ①l1与l2相交，交点为(s，t)；

    ②l1与l2相交，交点不一定是(s，t)；

    ③l1与l2必关于点(s，t)对称；

    ④l1与l2必定重合．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某服装商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系，随机统计了某4个月的月销售量与月平均气温，其数据如下表：

    月平均气温x/℃

    17

    13

    8

    2

    月销售量y/件

    24

    33

    40

    55

    由表中数据算出线性回归方程y＝bx＋a中的b≈－2.气象部门预测下个月的平均气温约为6 ℃，据此估计，该商场下个月毛衣的销售量约为________件．(参考公式：b＝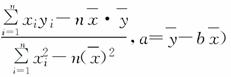

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某种产品的广告费支出x(单位：百万元)与销售额y(单位：百万元)之间有如下对应数据：

     

    x

    2

    4

    5

    6

    8

    y

    30

    40

    60

    50

    70

    (1)试根据表中数据估计广告费支出1 000万元时的销售额；

    (2)若广告费支出1 000万元时的实际销售额为8 500万元，求误差．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在平面直角坐标系xOy中，直线l与抛物线y2＝4x相交于不同的A，B两点．

    (1)如果直线l过抛物线的焦点，求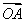·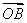的值；

    (2)如果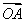·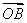＝－4，证明直线l必过一定点，并求出该定点．

    查看答案和解析>>

    同步练习册答案