为了研究两个变量x和y之间的线性相关性，甲、乙两位同学各自独立地做了10次和15次试验，并且利用线性回归方程，求得回归直线分别为l1和l2.已知两个人在试验中发现对变量x的观测数据的平均值都为s，对变量y的观测数据的平均值都为t，那么下列说法正确的是 ________．
①l1与l2相交，交点为(s，t)；
②l1与l2相交，交点不一定是(s，t)；
③l1与l2必关于点(s，t)对称；
④l1与l2必定重合．
科目：高中数学 来源： 题型：
7个人排成一排，在下列情况下，各有多少种不同排法？（写出解答过程及结果）
（1）甲排头: （1分） （2）甲不排头，也不排尾: （1分）
（3）甲、乙、丙三人必须在一起:（1分） （4）甲、乙之间有且只有两人: （1分）
（5）甲、乙、丙三人两两不相邻（2分） （6）甲在乙的左边（不一定相邻）（2分）
（7）甲、乙、丙三人按从高到矮，自左向右的顺序: （2分）
（8）甲不排头，乙不排当中:（2分）
解：（1）
（2）
（3）
（4）
（5）
（6）
（7）
（8）
查看答案和解析>>
科目：高中数学 来源： 题型：
设l为平面上过点(0，1)的直线，l的斜率等可能地取－2
，－
，－
，0，，，2，用ξ表示坐标原点到l的距离，则随机变量ξ的数学期望E(ξ)＝________.
查看答案和解析>>
科目：高中数学 来源： 题型：
如图2，一个小球从M处投入，通过管道自上而下落到A或B或C.已知小球从每个叉口落入左右两个管道的可能性是相等的．某商家按上述投球方式进行促销活动，若投入的小球落到A、B、C，则分别设为1，2，3等奖．
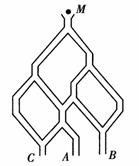
图2
(1)已知获得1，2，3等奖的折扣率分别为50%，70%，90%.记随变量ξ为获得k(k＝1，2，3)等奖的折扣率．求随机变量ξ的概率分布及期望E(ξ)；
(2)若有3人次(投入1球为1人次)参加促销活动，记随机变量η为获得1等奖或2等奖的人次，求P(η＝2)．
查看答案和解析>>
科目：高中数学 来源： 题型：
工人月工资(元)依劳动生产率(千元)变化的回归直线方程为
＝60＋90x，下列判断中正确的是 ________．
①劳动生产率为1 000元时，工资为50元；
②劳动生产率提高1 000元时，工资提高150元；
③劳动生产率提高1 000元时，工资提高90元；
④劳动生产率为1 000元时，工资为90元．
查看答案和解析>>
科目：高中数学 来源： 题型：
要分析学生初中升学的数学成绩对高一年级数学学习有什么影响，在高一年级学生中随机抽选10名学生分析他们入学的数学成绩和高一年级期末数学考试成绩，如下表所示．表中x是学生入学的数学成绩，y是高一年级期末考试数学成绩.
| x | 63 | 67 | 45 | 88 | 81 | 71 | 52 | 99 | 58 | 76 |
| y | 65 | 78 | 52 | 82 | 92 | 89 | 73 | 98 | 56 | 75 |
(1)画出散点图；
(2)求线性回归方程；
(3)若某学生王明亮的入学时的数学成绩为80分，试预测他在高一年级期末考试中的数学成绩为多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
利用独立性检验对两个研究对象是否有关系进行研究时，若有99.5%的把握认为A和B有关系，则具体计算出的数据应该是________．
①χ2≥6.635；②χ2<6.635；③χ2≥7.879；④χ2<7.879.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
是不相等的正实数，求证：
. 
是第二象限角，那么
是（ ）