
7个人排成一排,在下列情况下,各有多少种不同排法?(写出解答过程及结果)
(1)甲排头: (1分) (2)甲不排头,也不排尾: (1分)
(3)甲、乙、丙三人必须在一起:(1分) (4)甲、乙之间有且只有两人: (1分)
(5)甲、乙、丙三人两两不相邻(2分) (6)甲在乙的左边(不一定相邻)(2分)
(7)甲、乙、丙三人按从高到矮,自左向右的顺序: (2分)
(8)甲不排头,乙不排当中:(2分)
解:(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(1)甲固定不动,其余有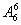 =720,即共有
=720,即共有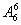 =720种;
=720种;
(2)甲有中间5个位置供选择,有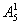 =5,其余有
=5,其余有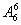 =720,即共有
=720,即共有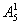
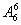 =3600种;
=3600种;
(3)先排甲、乙、丙三人,有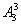 ,再把该三人当成一个整体,再加上另四人,相当 于5人的全排列,即
,再把该三人当成一个整体,再加上另四人,相当 于5人的全排列,即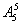 ,则共有
,则共有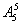
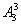 =720种;
=720种;
(4)从甲、乙之外的5人中选2个人排甲、乙之间,有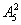 ,甲、乙可以交换有
,甲、乙可以交换有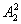 , 把该四人当成一个整体,再加上另三人,相当于4人的全排列, 则共有
, 把该四人当成一个整体,再加上另三人,相当于4人的全排列, 则共有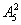
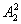
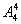 =960种;
=960种;
(5)先排甲、乙、丙之外的四人,有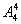 ,四人形成五个空位,甲、乙、丙三人排 这五个空位,有
,四人形成五个空位,甲、乙、丙三人排 这五个空位,有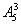 ,则共有
,则共有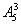
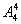 =1440种;
=1440种;
(6)不考虑限制条件有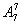 ,甲在乙的左边(不一定相邻),占总数的一半, 即
,甲在乙的左边(不一定相邻),占总数的一半, 即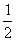
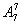 =2520种;
=2520种;
(7)先在7个位置上排甲、乙、丙之外的四人,有 ,留下三个空位,甲、乙、丙 三人按从高到矮,自左向右的顺序自动入列,不能乱排的,即
,留下三个空位,甲、乙、丙 三人按从高到矮,自左向右的顺序自动入列,不能乱排的,即 =840
=840
(8)不考虑限制条件有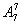 ,而甲排头有
,而甲排头有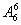 ,乙排当中有
,乙排当中有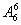 ,这样重复了甲排头, 乙排当中
,这样重复了甲排头, 乙排当中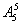 一次,即
一次,即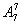 -2
-2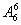 +
+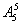 =3720
=3720


科目:高中数学 来源: 题型:
已知数列1,a+a2,a2+a3+a4,a3+a4+a5+a6,…,则数列的第k项是( )
A.ak+ak+1+…+a2k
B.ak-1+ak+…+a2k-1
C.ak-1+ak+…+a2k
D.ak-1+ak+…+a2k-2
查看答案和解析>>
科目:高中数学 来源: 题型:
利用下列盈利表中的数据进行决策,应选择的方案是________.
|
盈利 概率 | A1 | A2 | A3 | A4 |
| 0.25 | 50 | 70 | -20 | 98 |
| 0.30 | 65 | 26 | 52 | 82 |
| 0.45 | 26 | 16 | 78 | -10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
为了研究两个变量x和y之间的线性相关性,甲、乙两位同学各自独立地做了10次和15次试验,并且利用线性回归方程,求得回归直线分别为l1和l2.已知两个人在试验中发现对变量x的观测数据的平均值都为s,对变量y的观测数据的平均值都为t,那么下列说法正确的是 ________.
①l1与l2相交,交点为(s,t);
②l1与l2相交,交点不一定是(s,t);
③l1与l2必关于点(s,t)对称;
④l1与l2必定重合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com