
如图,将边长为1的正方形ABCD沿对角线AC折起,使得平面ADC⊥平面ABC,在折起后形成的三棱锥D-ABC中,给出下列三个命题:
①△DBC是等边三角形;
②AC⊥BD;
③三棱锥D-ABC的体积是![]() .
.

其中正确命题的序号是________.(写出所有正确命题的序号)
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
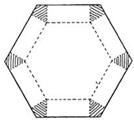
 如图,将边长为1的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正六棱柱容器.当这个正六棱柱容器的底面边长为
如图,将边长为1的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正六棱柱容器.当这个正六棱柱容器的底面边长为
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源:2012年苏教版高中数学选修2-21.4导数在实际生活的实际应用练习卷(解析版) 题型:填空题
如图,将边长为1的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正六棱柱容器(图).当这个正六棱柱容器的底面边长为 时,其容积最大.


查看答案和解析>>
科目:高中数学 来源:福建 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com