练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在4月份（共30天），有一新款服装投放某专卖店销售，日销售量（单位为件）f(x)关于时间n(1≤v≤30,n∈N*)的函数关系如图所示，其中函数f(n)的图象中的点位于斜率为5和－3的两条直线上，两直线的交点的横坐标为m，且第m天日销售量最大.

    （1）求f(n)的表达式，及前m天的销售总数；

    （2）按规律，当该专卖店销售总数超过400件时，社会上流行该服装，而日销售量连续下降并低于30件时，该服装的流行会消失，试问该服装在社会上流行的天数是否会超过10天？并说明理由.

    答案：
    解析：

    		（1）由图形知，当1≤n≤m且n∈N*时，f(n)=5n－3.

    由f(m)=57得m=12.

    前12天的销售总量为

    5（1+2+3+…+12）－3×12=354件.

     (2)第13天的销售量为f(13)= －3×13+93=54件.

    而354+54>400件，

    ∴从第14天开始销售总量超过400件，即开始流行.

    设第n天的日销售量开始低于30件（12<n≤30），即f(n)=－3n+93<30，解得n>21.

    ∴从第22天开始日销售量低于30件，

    即流行时间为14号至21号.

    ∴该服装流行时间不超过10天.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：044

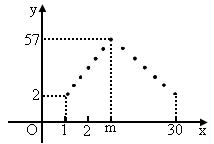
    在4月份（共30天），有一新款服装投放某专卖店销售，日销售量（单位为件）f(x)关于时间n(1≤v≤30,n∈N*)的函数关系如图所示，其中函数f(n)的图象中的点位于斜率为5和－3的两条直线上，两直线的交点的横坐标为m，且第m天日销售量最大.

    （1）求f(n)的表达式，及前m天的销售总数；

    （2）按规律，当该专卖店销售总数超过400件时，社会上流行该服装，而日销售量连续下降并低于30件时，该服装的流行会消失，试问该服装在社会上流行的天数是否会超过10天？并说明理由.

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：044

    在4月份(共30天)，有一新款服装投放某专卖店销售，日销售量(单位为件)f(n)关于时间n(1≤n≤30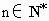，)的关系如图所示，其中函数f(n)图象中的点位于斜率为5和－3的两条直线上，两直线的交点的横坐标为m，且第m天日销售量最大．

    (1)求f(n)的表达式，及前m天的销售总数；

    (2)按规律，当该专卖店销售总数超过400件时，社会上流行该服装，而日销售量连续下降并低于30件时，该服装的流行会消失．试问该服装在社会上流行的天数是否会超过10天？并说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2011年福建省高二上学期期末考试数学理卷 题型：解答题

    （本题满分13分）在4月份（按30天计算），有一新款服装投入某商场销售，4月1日该款服装仅销售出10件，第二天售出35件，第三天销售60件，然后，每天售出的件数分别递增25件，直到4月12日销售量达到最大，以后每天销售的件数分别递减15件.

    （Ⅰ）问到月底该服装共销售出几件．

    （Ⅱ）按规律，当该商场销售此服装的日销售量达到150件以上时，社会上就流行，问该款服装在社会上流行是否超过14天？并说明理由.

     

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本题满分13分）在4月份（按30天计算），有一新款服装投入某商场销售，4月1日该款服装仅销售出10件，第二天售出35件，第三天销售60件，然后，每天售出的件数分别递增25件，直到4月12日销售量达到最大，以后每天销售的件数分别递减15件.

    （Ⅰ）问到月底该服装共销售出几件．

    （Ⅱ）按规律，当该商场销售此服装的日销售量达到150件以上时，社会上就流行，问该款服装在社会上流行是否超过14天？并说明理由.

    查看答案和解析>>

    同步练习册答案