
【题目】已知函数![]()
(I)讨论![]() 的单调性;
的单调性;
(II)当![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() ,都有
,都有![]() ?若存在求出
?若存在求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(I)当![]() ,
,![]() 在
在![]() 为增函数;当
为增函数;当![]() ,
,![]() 在
在![]() 为增函数,在
为增函数,在![]() 为减函数; (II)
为减函数; (II)![]() .
.
【解析】
(I)先求得函数![]() 的定义域,对其求导后对
的定义域,对其求导后对![]() 分成
分成![]() 两类,讨论函数的单调区间.(II)将不等式
两类,讨论函数的单调区间.(II)将不等式![]() 等价转化为
等价转化为![]() 恒成立,构造函数
恒成立,构造函数![]() ,利用其导数恒为非负数列不等式,分离常数后利用基本不等式求得
,利用其导数恒为非负数列不等式,分离常数后利用基本不等式求得![]() 的取值范围.
的取值范围.
(I)![]() 的定义域为
的定义域为![]()
![]() ,
,
当![]() ,则
,则![]() ,
,![]() 在
在![]() 为增函数,
为增函数,
![]() ,令
,令![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
所以,当![]()
![]() ,
,![]() ,
,![]() 在
在![]() 为增函数;
为增函数;
当![]()
![]() ,
,![]() ,
,![]() 在
在![]() 为减函数,
为减函数,
综上所述,当![]() ,
,![]() 在
在![]() 为增函数;
为增函数;
当![]() ,
,![]() 在
在![]() 为增函数,在
为增函数,在![]() 为减函数。
为减函数。
(II)不妨设![]() ,则
,则![]() ,
,
假设存在实数![]() ,使得
,使得![]()
![]() ,都有
,都有![]() ,
,
则![]() 恒成立,
恒成立,
即![]() 恒成立,(*)
恒成立,(*)
设![]() ,即(*)等价于
,即(*)等价于![]() 在
在![]() 为单调递增
为单调递增
等价于![]() 在
在![]() 恒成立,
恒成立,
等价于![]() 在
在![]() 恒成立,
恒成立,
等价于![]() 在
在![]() 恒成立,
恒成立,
∴![]() ,当且仅当
,当且仅当![]() 取等号,
取等号,
∴![]() ,∴
,∴![]() 的取值范围为
的取值范围为![]()


 新课标同步训练系列答案
新课标同步训练系列答案科目:高中数学 来源: 题型:
【题目】比较甲、乙两名学生的数学学科素养的各项能力指标值(满分为5分,分值高者为优),绘制了如图所示的六维能力雷达图,例如图中甲的数学抽象指标值为4,乙的数学抽象指标值为5,则下面叙述正确的是( )
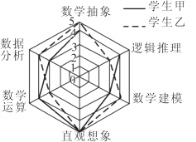
A.甲的逻辑推理能力指标值优于乙的逻辑推理能力指标值
B.甲的数学建模能力指标值优于乙的直观想象能力指标值
C.甲的六维能力指标值整体水平优于乙的六维能力指标值整体水平
D.甲的数学运算能力指标值优于甲的直观想象能力指标值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x),当年产量不足80千件时,C(x)=![]() x2+10x(万元).当年产量不小于80千件时,C(x)=51x+
x2+10x(万元).当年产量不小于80千件时,C(x)=51x+![]() -1 450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
-1 450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式;
(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知六棱锥![]() 的底面是正六边形,
的底面是正六边形,![]() 平面ABC,
平面ABC,![]() .则下列命题中正确的有( )
.则下列命题中正确的有( )
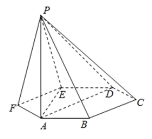
①平面![]() 平面PAE;
平面PAE;
②![]() ;
;
③直线CD与PF所成角的余弦值为![]() ;
;
④直线PD与平面ABC所成的角为45°;
⑤![]() 平面PAE.
平面PAE.
A.①④B.①③④C.②③⑤D.①②④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C经过点A(﹣1,3),B(3,3)两点,且圆心C在直线x﹣y+1=0上.
(1)求圆C的方程;
(2)求经过圆上一点A(﹣1,3)的切线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2,AB=1.
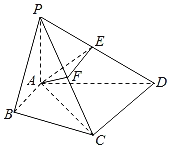
(Ⅰ)求四棱锥P﹣ABCD的体积V;
(Ⅱ)若F为PC的中点,求证:平面PAC⊥平面AEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,直线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数).以原点为极点,
为参数).以原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知与直线![]() 平行的直线
平行的直线![]() 过点
过点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,试求
两点,试求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】P是圆![]() 上的动点,P点在x轴上的射影是D,点M满足
上的动点,P点在x轴上的射影是D,点M满足![]() .
.
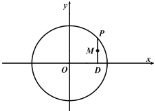
(1)求动点M的轨迹C的方程,并说明轨迹是什么图形;
(2)过点![]() 的直线l与动点M的轨迹C交于不同的两点A,B,求以OA,OB为邻边的平行四边形OAEB的顶点E的轨迹方程.
的直线l与动点M的轨迹C交于不同的两点A,B,求以OA,OB为邻边的平行四边形OAEB的顶点E的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com