

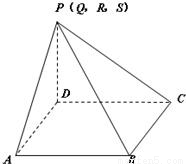
 解:(Ⅰ)它是有一条侧棱垂直于底面的四棱锥
解:(Ⅰ)它是有一条侧棱垂直于底面的四棱锥 ×6×6×6=72
×6×6×6=72 BC,
BC, BC,
BC, 在RT△PDC中,PD=DC
在RT△PDC中,PD=DC

 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:
 如图某一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,BQ=BR,点S、D、A、Q共线及P、D、C、R共线.
如图某一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,BQ=BR,点S、D、A、Q共线及P、D、C、R共线.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图某一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S、D、A、Q及P、D、C、R共线.
如图某一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S、D、A、Q及P、D、C、R共线.| PA |
查看答案和解析>>
科目:高中数学 来源: 题型:

![]() (本小题满分14分)如图某一几何体的展开图,其中
(本小题满分14分)如图某一几何体的展开图,其中![]() 是边长为6的正方形,
是边长为6的正方形,![]() ,
,![]() ,
,![]() ,点
,点![]() 、
、![]() 、
、![]() 、
、![]() 及
及![]() 、
、![]() 、
、![]() 、
、![]() 共线.(Ⅰ)沿图中虚线将它们折叠起来,使
共线.(Ⅰ)沿图中虚线将它们折叠起来,使![]() 、
、![]() 、
、![]() 、
、![]() 四点重合为点
四点重合为点![]() ,请画出其直观图;
,请画出其直观图;
(Ⅱ)求二面角![]() 的大小;(Ⅲ)试问需要几个这样的几何体才能拼成一个棱长为6的正方体
的大小;(Ⅲ)试问需要几个这样的几何体才能拼成一个棱长为6的正方体![]() ?
?
查看答案和解析>>
科目:高中数学 来源:2010年福建师大附中高考数学模拟试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com