
 的右焦点,过椭圆中心作一直线与椭圆交于P,Q两点,当三角形PFQ的面积最大时,
的右焦点,过椭圆中心作一直线与椭圆交于P,Q两点,当三角形PFQ的面积最大时,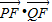 的值为 .
的值为 . 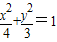 的右焦点F(1,0),要求△PQF的面积的最大值,需要先表示该三角形的面积,故需要设直线PQ的方程,分类讨论①当直线PQ的斜率存在时,设直线PQ的方程为y=kx(k≠0),代入椭圆方程,根据方程及弦长公式可求
的右焦点F(1,0),要求△PQF的面积的最大值,需要先表示该三角形的面积,故需要设直线PQ的方程,分类讨论①当直线PQ的斜率存在时,设直线PQ的方程为y=kx(k≠0),代入椭圆方程,根据方程及弦长公式可求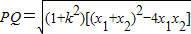 ,再求原点到AB的距离d=|
,再求原点到AB的距离d=|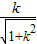 |,代入面积公式
|,代入面积公式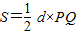 可求,②当直线的斜率不存在时,P(0,
可求,②当直线的斜率不存在时,P(0,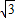 ),Q(0,-
),Q(0,-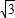 ),S=
),S=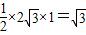 ,比较确定取得面积的最大值的点P,Q,代入
,比较确定取得面积的最大值的点P,Q,代入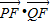 可求
可求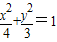 的右焦点F(1,0)
的右焦点F(1,0)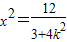
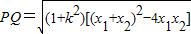 =
=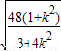
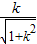 |
|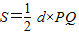 =|
=|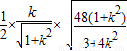 |=|
|=|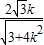 |=
|=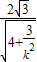 <
<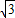
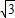 ),Q(0,-
),Q(0,-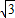 ),S=
),S=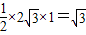
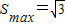 ,此时
,此时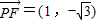 ,
,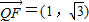
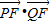 =1×1-
=1×1-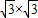 =-2
=-2

科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| MF |
| FN |
| AM |
| AN |
| 106 |
| 3 |
| AM |
| AN |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 12 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源:2008-2009学年重庆市南开中学高二(上)期中数学试卷(理科)(解析版) 题型:选择题
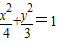 的右焦点,则该椭圆上与点F的距离最远的点到椭圆右准线的距离为( )
的右焦点,则该椭圆上与点F的距离最远的点到椭圆右准线的距离为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com