练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知数列{an}是等差数列，从a1，a2，a3，a4，a5，a6，a7中取走任意四项，则剩下三项构成等差数列的概率为( )

    A. B.

    C．1或 D．1或

    【答案】C

    【解析】当等差数列{an}的公差为0时，剩下三项一定构成等差数列，故概率为1.

    当等差数列{an}的公差不为0时，从a1，a2，a3，a4，a5，a6，a7中取走任意四项，剩下三项的总数有C＝35(种)，剩下三项构成等差数列，则符合条件的有(a1，a2，a3)，(a2，a3，a4)，(a3，a4，a5)，(a4，a5，a6)，(a5，a6，a7)，(a1，a3，a5)，(a2，a4，a6)，(a3，a5，a7)，(a1，a4，a7)9种情况，故剩下三项构成等差数列的概率为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】为了研究“教学方式”对教学质量的影响，某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学（勤奋程度和自觉性都一样）.以下茎叶图为甲、乙两班（每班均为20人）学生的数学期末考试成绩．

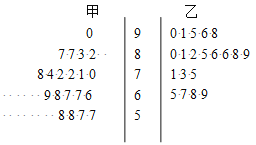
    （1）学校规定：成绩不低于75分的为优秀．请画出下面的列联表．

    甲班

    乙班

    合计

    优秀

    不优秀

    合计

    （2）判断有多大把握认为“成绩优秀与教学方式有关”．

    下面临界值表仅供参考：

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    参考公式：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分16分）已知是虚数， 是实数．

    （1）求为何值时， 有最小值，并求出|的最小值；

    （2）设，求证： 为纯虚数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C：＋＝1(a>b>0)的两个焦点分别为F1(－1，0)，F2(1，0)，且椭圆C经过点P.

    (1)求椭圆C的离心率；

    (2)设过点A(0，2)的直线l与椭圆C交于M，N两点，点Q是线段MN上的点，且＝＋，求点Q的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）求函数的图象在处的切线方程；

    （2）若函数在上有两个不同的零点，求实数的取值范围；

    （3）是否存在实数，使得对任意的，都有函数的图象在的图象的下方？若存在，请求出最大整数的值；若不存在，请说理由.

    （参考数据： ， ）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】根据某电子商务平台的调查统计显示，参与调查的1 000位上网购物者的年龄情况如图所示．

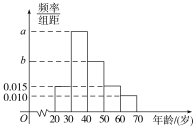
    (1)已知[30，40)，[40，50)，[50，60)三个年龄段的上网购物者人数成等差数列，求a，b的值；

    (2)该电子商务平台将年龄在[30，50)内的人群定义为高消费人群，其他年龄段的人群定义为潜在消费人群，为了鼓励潜在消费人群的消费，该平台决定发放代金券，高消费人群每人发放50元的代金券，潜在消费人群每人发放100元的代金券，现采用分层抽样的方式从参与调查的1 000位上网购物者中抽取10人，并在这10人中随机抽取3人进行回访，求此3人获得代金券总和X(单位：元)的分布列与数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆（）的离心率为，短轴的一个端点为.过椭圆左顶点的直线与椭圆的另一交点为.

    （1）求椭圆的方程；

    （2）若与直线交于点，求的值；

    （3）若，求直线的倾斜角.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列命题：

    ①若(1－x)5＝a0＋a1x＋a2x2＋a3x3＋a4x4＋a5x5，则|a1|＋|a2|＋|a3|＋|a4|＋|a5|＝32

    ②α，β，γ是三个不同的平面，则“γ⊥α，γ⊥β”是“α∥β”的充分条件

    ③已知sin＝，则cos＝.其中正确命题的个数为( )

    A．0 B．1

    C．2 D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝m－|x－1|－|x－2|，m∈R，且f(x＋1)≥0的解集为[0，1]．

    (1)求m的值；

    (2)若a，b，c，x，y，z∈R，且x2＋y2＋z2＝a2＋b2＋c2＝m，求证：ax＋by＋cz≤1.

    查看答案和解析>>

    同步练习册答案