
已知椭圆
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,椭圆上的点
,椭圆上的点 满足
满足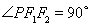 ,且
,且 的面积
的面积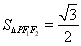 .
.
(Ⅰ)求椭圆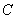 的方程;
的方程;
(Ⅱ)是否存在直线 ,使
,使 与椭圆
与椭圆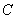 交于不同的两点
交于不同的两点 、
、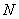 ,且线段
,且线段 恰被直线
恰被直线 平分?若存在,求出
平分?若存在,求出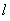 的斜率取值范围;若不存在,请说明理由.
的斜率取值范围;若不存在,请说明理由.
(I)椭圆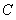 的方程为
的方程为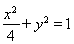 .(Ⅱ)存在满足题设条件的直线
.(Ⅱ)存在满足题设条件的直线 ,且
,且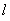 的斜率取值范围是
的斜率取值范围是
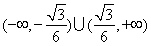 .
.
【解析】
试题分析:(Ⅰ)由题意知: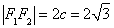 .
.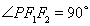 ,且
,且 ,由此可求得
,由此可求得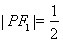 ,
,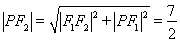 ,二者相加即得
,二者相加即得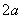 ,从而得椭圆的方程. (Ⅱ)假设这样的直线
,从而得椭圆的方程. (Ⅱ)假设这样的直线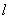 存在,且直线
存在,且直线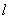 的方程为
的方程为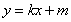 ,设
,设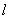 与椭圆
与椭圆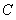 的两交点为
的两交点为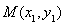 、
、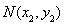 ,若线段
,若线段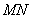 恰被直线
恰被直线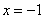 平分,则
平分,则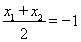 .这显然用韦达定理.由
.这显然用韦达定理.由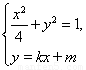 得
得 .
.
由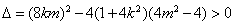 得
得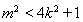 .再用韦达定理得
.再用韦达定理得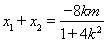 ,代入
,代入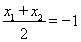 得
得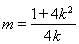 ,再将此式代入
,再将此式代入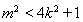 得一只含
得一只含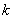 的不等式,解此不等式即得
的不等式,解此不等式即得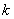 的取值范围.
的取值范围.
试题解析:(Ⅰ)由题意知: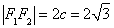 , (1分)
, (1分)
 椭圆上的点
椭圆上的点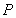 满足
满足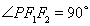 ,且
,且 ,
,
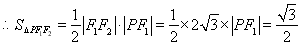 .
.
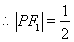 ,
,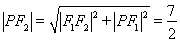 .
.
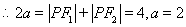 . (2分)
. (2分)
又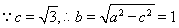 . (3分)
. (3分)
 椭圆
椭圆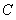 的方程为
的方程为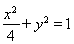 . (4分)
. (4分)
(Ⅱ)假设这样的直线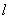 存在.
存在.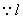 与直线
与直线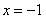 相交,
相交, 直线
直线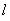 的斜率存在.
的斜率存在.
设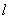 的方程为
的方程为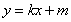 , (5分)
, (5分)
由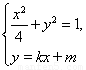 得
得 .(*) (6分)
.(*) (6分)
 直线
直线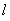 与椭圆
与椭圆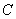 有两个交点,
有两个交点,
 (*)的判别式
(*)的判别式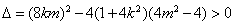 ,即
,即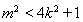 .① (7分)
.① (7分)
设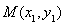 、
、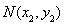 ,则
,则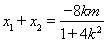 . (8分)
. (8分)
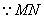 被直线
被直线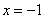 平分,可知
平分,可知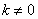 ,
,
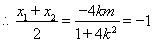 ,
,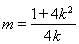 . ② (9分)
. ② (9分)
把②代入①,得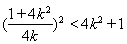 ,即
,即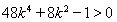 . (10分)
. (10分)
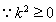 ,
,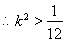 . (11分)
. (11分)
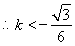 或
或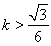 .即存在满足题设条件的直线
.即存在满足题设条件的直线 ,且
,且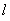 的斜率取值范围是
的斜率取值范围是
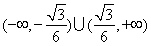 . (12分)
. (12分)
考点:直线与圆锥曲线.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,其右准线上
,其右准线上![]() 上存在点
上存在点![]() (点
(点![]() 在
在![]() 轴上方),使
轴上方),使![]() 为等腰三角形.
为等腰三角形.
⑴求离心率![]() 的范围;
的范围;
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三下学期假期检测考试理科数学试卷 题型:解答题
已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
点
,
点 是椭圆的一个顶点,△
是椭圆的一个顶点,△ 是等腰直角三角形.
是等腰直角三角形.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点 分别作直线
分别作直线 ,
, 交椭圆于
交椭圆于 ,
, 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为 ,
, ,且
,且 ,证明:直线
,证明:直线 过定点(
过定点( ).
).
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省三明市高三上学期三校联考数学理卷 题型:解答题
(本题满分14分) 已知椭圆 的左、右焦点分别为F1、F2,其中
的左、右焦点分别为F1、F2,其中
F2也是抛物线 的焦点,M是C1与C2在第一象限的交点,且
的焦点,M是C1与C2在第一象限的交点,且
(I)求椭圆C1的方程; (II)已知菱形ABCD的顶点A、C在椭圆C1上,顶点B、D在直线 上,求直线AC的方程。
上,求直线AC的方程。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年云南省德宏州高三高考复习数学试卷 题型:解答题
(本小题满分12分)
已知椭圆 的左、右焦点分别为
的左、右焦点分别为 、
、 ,离心率
,离心率 ,右准线方程为
,右准线方程为 .
.
(I)求椭圆的标准方程;
(II)过点 的直线
的直线 与该椭圆交于M、N两点,且
与该椭圆交于M、N两点,且 ,求直线
,求直线 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com