
 是定义在(-1,1)上的奇函数,且
是定义在(-1,1)上的奇函数,且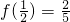 .
. 是定义在(-1,1)上的奇函数,
是定义在(-1,1)上的奇函数,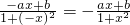
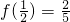
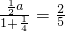
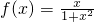
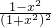
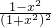 >0
>0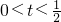
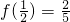 可求a,进而可求函数解析式
可求a,进而可求函数解析式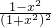 ,结合已知x的范围判断导函数的正负即可判断函数f(x)在(-1,1)上的单调性
,结合已知x的范围判断导函数的正负即可判断函数f(x)在(-1,1)上的单调性

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源:2010-2011学年河南省商丘市虞城二高高一(上)期中数学试卷(解析版) 题型:解答题
 是定义在(-1,1)上的奇函数,且
是定义在(-1,1)上的奇函数,且 .
.查看答案和解析>>
科目:高中数学 来源:2015届重庆市高一10月月考数学试卷(解析版) 题型:解答题
(12分)已知函数 是定义在(–1,1)上的奇函数,且
是定义在(–1,1)上的奇函数,且 .
.
(1)求函数f(x)的解析式;
(2)判断函数f(x)在(–1,1)上的单调性并用定义证明;
(3)解关于x的不等式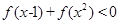
查看答案和解析>>
科目:高中数学 来源:2010年河南大学附属中学(本部)高一上学期期中考试数学卷 题型:解答题
(本题满分12分)
已知函数 是定义在(–1,1)上的奇函数,且
是定义在(–1,1)上的奇函数,且 ,
,
①求函数f(x)的解析式;
②判断函数f(x)在(–1,1)上的单调性并用定义证明;
③解关于x的不等式 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com