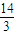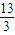【答案】
分析:本题考查的知识点是线性规划,处理的思路为:根据已知的约束条件,画出满足约束条件的可行域,再
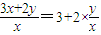
,分析

表示的几何意义,结合图象即可给出
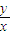
的最大值.
解答: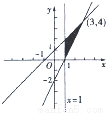
解::先根据实数x,y满足的条件画出可行域,
由于
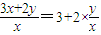
,
而
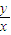
的几何意义是可行域内任意一点P与坐标原点连线的斜率
观察图形可知,当点P在点(1,2)处
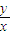
取最大值
最大值为2,则

的最大值是3+4=7
故选D.
点评:平面区域的最值问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,分析表达式的几何意义,然后结合数形结合的思想,分析图形,找出满足条件的点的坐标,即可求出答案.

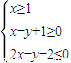 则
则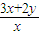 的最大值是( )
的最大值是( )