
【题目】已知椭圆C1: ![]() +y2=1,椭圆C2以C1的长轴为短轴,且与C1有相同的离心率.
+y2=1,椭圆C2以C1的长轴为短轴,且与C1有相同的离心率.
(1)求椭圆C2的方程;
(2)设O为坐标原点,点A,B分别在椭圆C1和C2上, ![]() =2
=2 ![]() ,求直线AB的方程.
,求直线AB的方程.
【答案】
(1)解:椭圆 ![]() 的长轴长为4,离心率为
的长轴长为4,离心率为 ![]()
∵椭圆C2以C1的长轴为短轴,且与C1有相同的离心率
∴椭圆C2的焦点在y轴上,2b=4,为 ![]()
∴b=2,a=4
∴椭圆C2的方程为 ![]() ;
;
(2)解:设A,B的坐标分别为(xA,yA),(xB,yB),
∵ ![]() =2
=2 ![]()
∴O,A,B三点共线,且点A,B不在y轴上
∴设AB的方程为y=kx
将y=kx代入 ![]() ,消元可得(1+4k2)x2=4,∴
,消元可得(1+4k2)x2=4,∴ ![]()
将y=kx代入 ![]() ,消元可得(4+k2)x2=16,∴
,消元可得(4+k2)x2=16,∴ ![]()
∵ ![]() =2
=2 ![]() ,∴
,∴ ![]() =4
=4 ![]() ,
,
∴ ![]() ,解得k=±1,
,解得k=±1,
∴AB的方程为y=±x
【解析】(1)求出椭圆 ![]() 的长轴长,离心率,根据椭圆C2以C1的长轴为短轴,且与C1有相同的离心率,即可确定椭圆C2的方程;(2)设A,B的坐标分别为(xA , yA),(xB , yB),根据
的长轴长,离心率,根据椭圆C2以C1的长轴为短轴,且与C1有相同的离心率,即可确定椭圆C2的方程;(2)设A,B的坐标分别为(xA , yA),(xB , yB),根据 ![]() =2
=2 ![]() ,可设AB的方程为y=kx,分别与椭圆C1和C2联立,求出A,B的横坐标,利用
,可设AB的方程为y=kx,分别与椭圆C1和C2联立,求出A,B的横坐标,利用 ![]() =2
=2 ![]() ,即可求得直线AB的方程.
,即可求得直线AB的方程.
【考点精析】利用椭圆的标准方程对题目进行判断即可得到答案,需要熟知椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
【题目】为了调查我市在校中学生参加体育运动的情况,从中随机抽取了16名男同学和14 名女同学,调查发现,男、女同学中分别有12人和6人喜爱运动,其余不喜爱.
(1)根据以上数据完成以下![]() 列联表:
列联表:
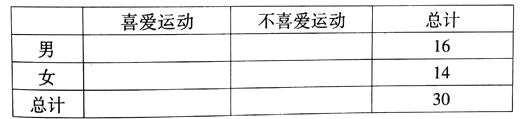
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.010的前提下认为性别与喜爱运动有关?
(3)将以上统计结果中的频率视作概率,从我市中学生中随机抽取3人,若其中喜爱运动的人数为![]() ,求
,求![]() 的分布列和均值.
的分布列和均值.
参考数据:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,如图是根据调查结果绘制的选手等级人数的条形图.

(1)若将一般等级和良好等级合称为合格等级,根据已知条件完成![]() 列联表,并据此资料你是否有
列联表,并据此资料你是否有![]() 的把握认为选手成绩“优秀”与文化程度有关?
的把握认为选手成绩“优秀”与文化程度有关?

注:![]() ,其中
,其中![]() .
.

(2)若江西参赛选手共80人,用频率估计概率,试估计其中优秀等级的选手人数;
(3)如果在优秀等级的选手中取4名,在良好等级的选手中取2名,再从这6人中任选3人组成一个比赛团队,求所选团队中有2名选手的等级为优秀的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,过点
中,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校选派甲、乙、丙、丁、戊5名学生代表学校参加市级“演讲”和“诗词”比赛,下面是他们的一段对话.甲说:“乙参加‘演讲’比赛”;乙说:“丙参加‘诗词’比赛”;丙说“丁参加‘演讲’比赛”;丁说:“戊参加‘诗词’比赛”;戊说:“丁参加‘诗词’比赛”.
已知这5个人中有2人参加“演讲”比赛,有3人参加“诗词”比赛,其中有2人说的不正确,且参加“演讲”的2人中只有1人说的不正确.根据以上信息,可以确定参加“演讲”比赛的学生是
A. 甲和乙 B. 乙和丙 C. 丁和戊 D. 甲和丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】符号![]() 表示不大于
表示不大于![]() 的最大整数(
的最大整数(![]() ),例如:
),例如:![]()
(1)已知![]() ,分别求两方程的解集
,分别求两方程的解集![]() ;
;
(2)设方程![]() 的解集为
的解集为![]() ,集合
,集合![]() ,若
,若![]() ,求
,求![]() 的取值范围.
的取值范围.
(3)在(2)的条件下,集合![]() ,是否存在实数
,是否存在实数![]() ,
,![]() ,若存在,请求出实数
,若存在,请求出实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)求证: ![]() .
.
(2)某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:
sin213°+cos217°-sin13°cos17°;
sin215°+cos215°-sin15°cos15°;
sin218°+cos212°-sin18°cos12°;
sin2(-18°)+cos248°-sin(-18°)cos48°;
sin2(-25°)+cos255°-sin(-25°)cos55°.
①试从上述五个式子中选择一个,求出这个常数;
②根据①的计算结果,将该同学的发现推广为三角恒等式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级举行了一次全年级的大型考试,在数学成绩优秀和非优秀的学生中,物理、化学、总分成绩也为优秀的人数如下表所示,则我们能以99%的把握认为数学成绩优秀与物理、化学、总分成绩优秀有关系吗?
物理优秀 | 化学优秀 | 总分优秀 | |
数学优秀 | 228 | 225 | 267 |
数学非优秀 | 143 | 156 | 99 |
注:该年级此次考试中数学成绩优秀的有360人,非优秀的有880人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com