
已知直线l经过点P(1,1),倾斜角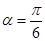 .
.
(1)写出直线l的参数方程;
(2)设l与圆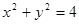 相交于两点A,B,求点P到A,B两点的距离之积.
相交于两点A,B,求点P到A,B两点的距离之积.
(1)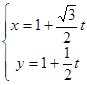 ;(2)点P到A,B两点的距离之积为2.
;(2)点P到A,B两点的距离之积为2.
解析试题分析:(1)利用公式和已知条件直线l经过点P(1,1),倾斜角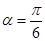 ,写出其极坐标再化为一般参数方程;
,写出其极坐标再化为一般参数方程;
(2)由题意将直线代入x2+y2=4,从而求解.
(1)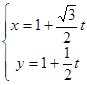 ;---------------5分
;---------------5分
(2)把直线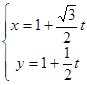 代入
代入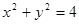 ,得:
,得: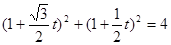
所以 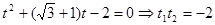 ,则点P到A,B两点的距离之积为2.----10分
,则点P到A,B两点的距离之积为2.----10分
考点:本题主要考查了参数方程与普通方程的区别和联系,两者要会互相转化,根据实际情况选择不同的方程进行求解,这也是每年高考必的热点问题。
点评:解决该试题的关键是利用直线方程得到其参数方程,联立方程组来得到参数t满足的关系式,进而运用参数的几何意义得到求解。


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:解答题
在平面直角坐标系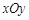 中,曲线
中,曲线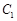 的参数方程为
的参数方程为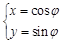 (
(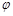 为参数),曲线
为参数),曲线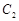 的参数方程为
的参数方程为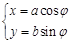 (
(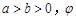 为参数).在以
为参数).在以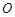 为极点,
为极点, 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线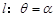 与
与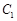 ,
,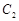 各有一个交点.当
各有一个交点.当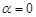 时,这两个交点间的距离为
时,这两个交点间的距离为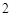 ,当
,当 时,这两个交点重合.
时,这两个交点重合.
(Ⅰ)分别说明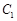 ,
,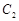 是什么曲线,并求出a与b的值;
是什么曲线,并求出a与b的值;
(Ⅱ)设当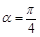 时,
时,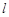 与
与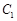 ,
,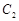 的交点分别为
的交点分别为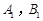 ,当
,当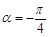 时,
时,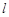 与
与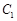 ,
,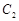 的交点分别为
的交点分别为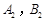 ,求四边形
,求四边形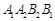 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
本小题满分10分)
已知直线l经过点P(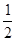 ,1),倾斜角
,1),倾斜角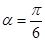 ,在极坐标系下,圆C的极坐标方程为
,在极坐标系下,圆C的极坐标方程为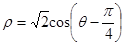 。
。
(1)写出直线l的参数方程,并把圆C的方程化为直角坐标方程;
(2)设l与圆C相交于A,B两点,求点P到A,B两点的距离之积。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)选修4-4:坐标系与参数方程
已知直线 的参数方程为:
的参数方程为:
 (t为参数),曲线C的极坐标方程为:
(t为参数),曲线C的极坐标方程为: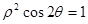 .
.
(1)求曲线C的普通方程;
(2)求直线 被曲线C截得的弦长.
被曲线C截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知曲线C: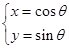 (
(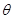 为参数).
为参数).
(1)将C的参数方程化为普通方程;
(2)若把C上各点的坐标经过伸缩变换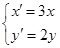 后得到曲线
后得到曲线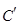 ,求曲线
,求曲线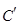 上任意一点到两坐标轴距离之积的最大值.
上任意一点到两坐标轴距离之积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本.若样本中的中年职工为5人,则样本容量为( )
| A.7 | B.15 | C.25 | D.35 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
为了从甲乙两人中选一人参加数学竞赛,老师将二人最近6次数学测试的分数进行统计,甲乙两人的平均成绩分别是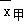 、
、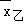 ,则下列说法正确的是( )
,则下列说法正确的是( )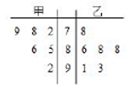
A.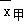 > >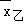 ,乙比甲成绩稳定,应选乙参加比赛 ,乙比甲成绩稳定,应选乙参加比赛 |
B.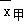 > >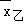 ,甲比乙成绩稳定,应选甲参加比赛 ,甲比乙成绩稳定,应选甲参加比赛 |
C.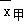 < <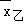 ,甲比乙成绩稳定,应选甲参加比赛 ,甲比乙成绩稳定,应选甲参加比赛 |
D.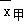 < <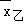 ,乙比甲成绩稳定,应选乙参加比赛 ,乙比甲成绩稳定,应选乙参加比赛 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
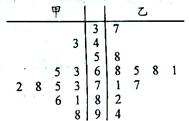
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,一般情况下PM2.5的浓度越大,大气环境质量越差.右边的茎叶图表示的是成都市区甲乙两个监测站某10日内每天的PM2.5浓度读数(单位: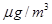 ),则下列说法正确的是( )
),则下列说法正确的是( )
| A.这10日内甲、乙监测站读数的极差相等 |
| B.这10日内甲、乙监测站读数的中位数中,乙的较大 |
| C.这10日内乙监测站读数的众数与中位数相等 |
| D.这10日内甲、乙监测站读数的平均数相等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com