
科目:高中数学 来源: 题型:
| ? |
| y |
. |
| x |
. |
| y |
查看答案和解析>>
科目:高中数学 来源: 题型:
| PD |
| PC |
| PA |
| PB |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2011•盐城二模)如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成.两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为r1=13; 圆弧C2过点A(29,0).
(2011•盐城二模)如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成.两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为r1=13; 圆弧C2过点A(29,0).| 30 |
查看答案和解析>>
科目:高中数学 来源:2010-2011常年江苏省高二年级第三次月考数学试题(理) 题型:填空题
以下结论正确的是
(1)根据2×2列联表中的数据计算得出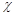 2≥6.635,
而P(
2≥6.635,
而P(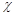 2≥6.635)≈0.01,则有99% 的把握认为两个分类变量有关系
2≥6.635)≈0.01,则有99% 的把握认为两个分类变量有关系
(2)在线性回归分析中,相关系数为r,|r|越接近于1,相关程度越大;|r|越小,相关程度越小
(3)在回归分析中,回归直线方程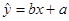 过点
过点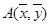
(4)在回归直线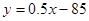 中,变量x=200时,变量y的值一定是15
中,变量x=200时,变量y的值一定是15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com