练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设ABCD－A1B1C1D1是棱长为1的正方体，则上底面ABCD的内切圆上的点P与过顶点A，B，C1，D1的圆上的点Q之间的最小距离是­­­­­­­­­­­­­­­­­­­­­___________.
    解析：设点O是正方体的中心，则易得OQ=，OP=，则由三角不等式PQ≥OQ－OP=．等号当且仅当三点O、P、Q共线时成立．又显然当点P为线段AB中点时，设射线OP与ABC1D1的外接圆的交点为Q时满足要求
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网如图，在棱长为a的正方体ABCD-A1B1C1D1中，M、N分别是AA1、D1C1的中点，过D、M、N三点的平面与正方体的下底面相交于直线l；
    （1）画出直线l；
    （2）设l∩A1B1=P，求PB1的长；
    （3）求D到l的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某房地产开发公司计划在一楼区内建造一个长方形公园ABCD，公园由长方形的休闲区A1B1C1D1（阴影部分）和环公园人行道组成．已知休闲区A1B1C1D1的面积为4000平方米，人行道的宽分别为4米和10米．
    （1）若设休闲区的长A1B1=x米，求公园ABCD所占面积S关于x的函数S（x）的解析式；
    （2）要使公园所占面积最小，休闲区A1B1C1D1的长和宽该如何设计？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

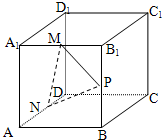    如图，正方体ABCD-A1B1C1D1的棱长为8，M，N，P分别是A1B1，AD，B B1的中点．
    （1）画出过点M，N，P的平面与平面ABCD的交线以及与平面BB1C1C的交线；
    （2）设平面PMN与棱BC交于点Q，求PQ的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

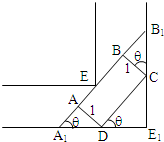    一条直角走廊宽 1.5米，如图所示，现有一转动灵活的手推车，其平板面为矩形ABCD，宽AD为1米，延长AB交直角走廊于A1、B1，设∠CDE1=θ，
    （1）证明：A1B1=1.5（
    1
    sinθ
    +
    1
    cosθ
    ）．
    （2）求A1B1的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，在棱长为a的正方体ABCD—A1B1C1D1中，M、N分别是AA1、D1C1的中点，过D、M、N三点的平面与正方体的下底面相交于直线l；

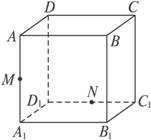
     (1)画出直线l；

    (2)设l∩A1B1=P,求PB1的长；

    (3)求D到l的距离.

    查看答案和解析>>

    同步练习册答案