
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)当函数![]() 与函数
与函数![]() 图象的公切线l经过坐标原点时,求实数a的取值集合;
图象的公切线l经过坐标原点时,求实数a的取值集合;
(3)证明:当![]() 时,函数
时,函数![]() 有两个零点
有两个零点![]() ,
,![]() ,且满足
,且满足![]() .
.
【答案】(1)单调增区间为![]() ,单调减区间为
,单调减区间为![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)利用导数求解单调性;(2)先求出公切线![]() 的方程,再探讨
的方程,再探讨![]() 的取值范围;(3)先利用导数研究函数
的取值范围;(3)先利用导数研究函数![]() 的单调性,证明零点个数.再使用函数思想,构造函数,利用导数研究函数单调性解决不等式问题.
的单调性,证明零点个数.再使用函数思想,构造函数,利用导数研究函数单调性解决不等式问题.
(1)对![]() 求导,得
求导,得![]() ,
,
令![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
当![]() ,
,![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
(2)设公切线![]() 与函数
与函数![]() 的切点为
的切点为![]() ,
,![]() ,则公切线
,则公切线![]() 的斜率
的斜率![]() ,
,
公切线![]() 的方程为:
的方程为:![]() ,将原点坐标
,将原点坐标![]() 代入,得
代入,得![]() ,解得
,解得![]() .
.
公切线![]() 的方程为:
的方程为:![]() ,将它与
,将它与![]() 联立,整理得
联立,整理得![]() .
.
令![]() ,对之求导得:
,对之求导得:![]() ,令
,令![]() ,解得
,解得![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递减,值域为
单调递减,值域为![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增,值域为
单调递增,值域为![]() ,
,
由于直线![]() 与函数
与函数![]() 相切,即只有一个公共点,因此.
相切,即只有一个公共点,因此.
故实数![]() 的取值集合为
的取值集合为![]() .
.
(3)证明:![]() ,要证
,要证![]() 有两个零点,只要证
有两个零点,只要证![]() 有两个零点即可.
有两个零点即可.![]() (1)
(1)![]() ,
,
即![]() 时函数
时函数![]() 的一个零点.
的一个零点.
对![]() 求导得:
求导得:![]() ,令
,令![]() ,解得
,解得![]() .当
.当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减.当
单调递减.当![]() 时,
时,![]() 取最小值,
取最小值,![]() ,
,
![]() ,必定存
,必定存![]() 在使得二次函数
在使得二次函数![]() ,
,
即![]() .因此在区间上
.因此在区间上![]() 必定存在
必定存在![]() 的一个零点.
的一个零点.
综上所述,![]() 有两个零点,一个是
有两个零点,一个是![]() ,另一个在区间
,另一个在区间![]() 上.
上.
下面证明![]() .
.
由上面步骤知![]() 有两个零点,一个是
有两个零点,一个是![]() ,另一个在区间
,另一个在区间![]() 上.
上.
不妨设![]() ,
,![]() 则
则![]() ,下面证明
,下面证明![]() 即可.
即可.
令![]() ,对之求导得
,对之求导得![]() ,
,
故![]() (a)在定义域内单调递减,
(a)在定义域内单调递减,![]() ,即
,即![]() .
.
证明完毕.


科目:高中数学 来源: 题型:
【题目】《算法统宗》全称《新编直指算法统宗》,是屮国古代数学名著,程大位著.书中有如下问题:“今有五人均银四十两,甲得十两四钱,戊得五两六钱.问:次第均之,乙丙丁各该若干?”意思是:有5人分40两银子,甲分10两4钱,戊分5两6钱,且相邻两项差相等,则乙丙丁各分几两几钱?(注:1两等于10钱)( )
A.乙分8两,丙分8两,丁分8两B.乙分8两2钱,丙分8两,丁分7两8钱
C.乙分9两2钱,丙分8两,丁分6两8钱D.乙分9两,丙分8两,丁分7两
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某基地蔬菜大棚采用水培、无土栽培方式种植各类蔬菜.过去50周的资料显示,该地周光照量![]() (小时)都在30小时以上,其中不足50小时的周数有5周,不低于50小时且不超过70小时的周数有35周,超过70小时的周数有10周.根据统计,该基地的西红柿增加量
(小时)都在30小时以上,其中不足50小时的周数有5周,不低于50小时且不超过70小时的周数有35周,超过70小时的周数有10周.根据统计,该基地的西红柿增加量![]() (百斤)与使用某种液体肥料
(百斤)与使用某种液体肥料![]() (千克)之间对应数据为如图所示的折线图.
(千克)之间对应数据为如图所示的折线图.

(1)依据数据的折线图,是否可用线性回归模型拟合![]() 与
与![]() 的关系?请计算相关系数
的关系?请计算相关系数![]() 并加以说明(精确到0.01).(若
并加以说明(精确到0.01).(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
(2)蔬菜大棚对光照要求较大,某光照控制仪商家为该基地提供了部分光照控制仪,但每周光照控制仪最多可运行台数受周光照量![]() 限制,并有如下关系:
限制,并有如下关系:
周光照量 |
|
|
|
光照控制仪最多可运行台数 | 3 | 2 | 1 |
若某台光照控制仪运行,则该台光照控制仪周利润为3000元;若某台光照控制仪未运行,则该台光照控制仪周亏损1000元.若商家安装了3台光照控制仪,求商家在过去50周周总利润的平均值.
附:相关系数公式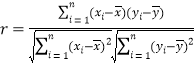 ,参考数据
,参考数据![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 与曲线
与曲线![]() ,(
,(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)写出曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)在极坐标系中,已知![]() 与
与![]() ,
,![]() 的公共点分别为
的公共点分别为![]() ,
,![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代名著《张丘建算经》中记载:“今有方锥,下广二丈,高三丈.欲斩末为方亭,令上方六尺.问:斩高几何?”大致意思是:有一个正四棱锥下底边长为二丈,高三丈,现从上面截去一段,使之成为正四棱台,且正四棱台的上底边长为六尺,则截去的正四棱锥的高是多少.如果我们把求截去的正四棱锥的高改为求剩下的正四棱台的体积,则该正四棱台的体积是(注:1丈![]() 尺)( )
尺)( )
A.1946立方尺B.3892立方尺C.7784立方尺D.11676立方尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,
中,![]() 侧面
侧面![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,点E是棱
,点E是棱![]() 的中点.
的中点.

(1)求证:![]() 平面ABC;
平面ABC;
(2)在棱CA上是否存在一点M,使得EM与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com