
【题目】已知函数![]() ,实数
,实数![]() 为常数).
为常数).
(1)若![]() ,且函数
,且函数![]() 在
在![]() 上的最小值为0,求
上的最小值为0,求![]() 的值;
的值;
(2)若对于任意的实数![]() ,函数
,函数![]() 在区间
在区间![]() 上总是减函数,对每个给定的
上总是减函数,对每个给定的![]() ,求
,求![]() 的最大值
的最大值![]() .
.
【答案】(1)![]() ;(2)
;(2)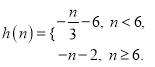 .
.
【解析】试题分析:(1)先求导,求函数在已知区间上的极值,注意极值点是否在定义域内,进行分类讨论,确定最小值,列出关于![]() 的方程即可得结果;(2)函数在区间上单调递减,转化为导函数小于等于0恒成立,再转化为二次函数根的分布问题.
的方程即可得结果;(2)函数在区间上单调递减,转化为导函数小于等于0恒成立,再转化为二次函数根的分布问题.
试题解析:(1)当![]() 时,
时, ![]() .
.
则![]() .
.
令![]() ,得
,得![]() (舍),
(舍),![]() .
.
①当![]() >1时,
>1时,
| 1 |
|
|
|
| - | 0 | + | |
|
| ↘ |
| ↗ |
∴当![]() 时,
时, ![]() .
.
令![]() ,得
,得![]() .
.
②当![]() 时,
时, ![]() ≥0在
≥0在![]() 上恒成立,
上恒成立,
![]() 在
在![]() 上为增函数,当
上为增函数,当![]() 时,
时, ![]() .
.
令![]() ,得
,得![]() (舍).
(舍).
综上所述,所求![]() 为
为![]() .
.
(2) ∵对于任意的实数![]() ,
, ![]() ,
, ![]() 在区间
在区间![]() 上总是减函数,
上总是减函数,
则对于x∈(1,3), ![]() <0,
<0,
∴![]() 在区间[1,3]上恒成立.
在区间[1,3]上恒成立.
设g(x)= ![]() ,∵
,∵![]() ,∴g(x)
,∴g(x) ![]() 在区间[1,3]上恒成立.
在区间[1,3]上恒成立.
由g(x)二次项系数为正,得
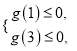 即
即![]() 亦即
亦即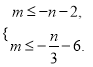
∵![]()
![]() =
=![]() ,
,
∴ 当n<6时,m≤![]() ,当n≥6时,m≤
,当n≥6时,m≤![]() ,
,
∴ 当n<6时,h(n)= ![]() ,当n≥6时,h(n)=
,当n≥6时,h(n)= ![]() ,
,
即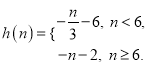


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:
【题目】设关于x的一元二次方程x2+2ax+b2=0.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.
(2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两所学校高三年级分别有1 200人,1 000人,为了了解两所学校全体高三年级学生在该地区六校联考的数学成绩情况,采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩,并作出了频数分布统计表如下:
甲校:
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 3 | 4 | 8 | 15 |
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 15 | x | 3 | 2 |
乙校:
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 1 | 2 | 8 | 9 |
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 10 | 10 | y | 3 |
则x,y的值分别为( )
(A)、12,7 (B)、 10,7 (C)、 10,8 (D)、 11,9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得 M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,则山高MN=m. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三角形的顶点分别为A(﹣1,3),B(3,2),C(1,0)
(1)求BC边上高的长度;
(2)若直线l过点C,且在l上不存在到A,B两点的距离相等的点,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com