
【题目】已知![]() ,其中
,其中![]() 是自然常数,
是自然常数, ![]()
(1)当![]() 时,求
时,求![]() 的单调性和极值;
的单调性和极值;
(2)若![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)减区间是, ![]() 增区间是
增区间是![]() ,
, ![]() 的极小值为
的极小值为![]() ,
, ![]() 无极大值;(2)
无极大值;(2)![]() .
.
【解析】试题分析:(1)当![]() 时,
时, ![]() ,求出
,求出![]() ,在定义域内解不等式,
,在定义域内解不等式, ![]() ,即可得到单调区间,由单调性即可得到极值;(2)
,即可得到单调区间,由单调性即可得到极值;(2)![]() 恒成立,即
恒成立,即![]() 恒成立,问题转化为求函数
恒成立,问题转化为求函数![]() 的最大值,利用导数研究函数的单调性即可求得.
的最大值,利用导数研究函数的单调性即可求得.
试题解析:(1) ![]() ,
,
∴当![]() 时,
时, ![]() ,此时
,此时![]() 为单调递减;
为单调递减;
当![]() 时,
时, ![]() ,此时
,此时![]() 为单调递增.
为单调递增.
∴当![]() 的极小值为
的极小值为![]() ,
, ![]() 无极大值.
无极大值.
(2)法一:∵![]() ,
,
∴![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,
, ![]() ,
,
∴![]()
令![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() ,此时
,此时![]() 为单调递增,
为单调递增,
当![]() 时,
时, ![]() ,此时
,此时![]() 为单调递减,
为单调递减,
∴![]() ,
,
∴![]() .
.
法二:由条件: ![]() 在
在![]() 上恒成立
上恒成立
令![]() ,
, ![]() ,
, ![]() ,
,
![]() 时,
时, ![]() 恒成立,∴
恒成立,∴![]() 在
在![]() 上递减,
上递减,
∴![]() ;
;
由条件知![]() ∴
∴![]() 与
与![]() 矛盾.
矛盾.
![]() 时,令
时,令![]() ,∴
,∴ ![]()
当![]() 时,
时, ![]() ,此时
,此时![]() 为单调递增,
为单调递增,
当![]() 时,
时, ![]() ,此时
,此时![]() 为单调递减,
为单调递减,
![]() ,
,
∴![]()
即![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD和ADPQ均为正方形,他们所在的平面互相垂直,动点M在线段PQ上,E,F分别为AB,BC的中点,设异面直线EM与AF所成的角为θ,则cosθ的最大值为 . 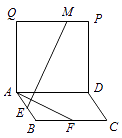
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,实数
,实数![]() 为常数).
为常数).
(1)若![]() ,且函数
,且函数![]() 在
在![]() 上的最小值为0,求
上的最小值为0,求![]() 的值;
的值;
(2)若对于任意的实数![]() ,函数
,函数![]() 在区间
在区间![]() 上总是减函数,对每个给定的
上总是减函数,对每个给定的![]() ,求
,求![]() 的最大值
的最大值![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(2cosx,
=(2cosx, ![]() sinx),
sinx), ![]() =(3cosx,﹣2cosx),设函数f(x)=
=(3cosx,﹣2cosx),设函数f(x)= ![]()
![]()
(1)求f(x)的最小正周期;
(2)若x∈[0, ![]() ],求f(x)的值域.
],求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,底面ABCD是边长为1的菱形, ![]() 底面ABCD,SA=2,M为SA的中点.
底面ABCD,SA=2,M为SA的中点. 
(1)求异面直线AB与MD所成角的大小;
(2)求直线AS与平面SCD所成角的正弦值;
(3)求平面SAB与平面SCD所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
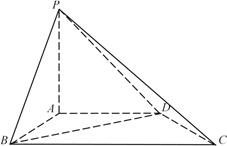
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥AD,AD∥BC,AP=AB=AD=1.
(Ⅰ)若直线PB与CD所成角的大小为![]() ,求BC的长;
,求BC的长;
(Ⅱ)求二面角B-PD-A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}和等比数列{bn},其中{an}的公差不为0.设Sn是数列{an}的前n项和.若a1 , a2 , a5是数列{bn}的前3项,且S4=16.
(1)求数列{an}和{bn}的通项公式;
(2)若数列{ ![]() }为等差数列,求实数t;
}为等差数列,求实数t;
(3)构造数列a1 , b1 , a2 , b1 , b2 , a3 , b1 , b2 , b3 , …,ak , b1 , b2 , …,bk , …,若该数列前n项和Tn=1821,求n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com