


 ,设
,设
(Ⅰ)求函数 的周期及单调增区间。
的周期及单调增区间。
(Ⅱ)设 的内角
的内角 的对边分别为
的对边分别为 ,已知
,已知
 ,求边
,求边 的值.
的值.
单调递增区间是[2k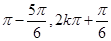 ],周期T=2
],周期T=2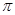 ;(Ⅱ)
;(Ⅱ)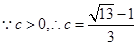
【解析】此题考查了正弦、余弦定理,三角函数的周期性及其求法,以及三角函数的恒等变换应用,涉及的知识有:两角和与差的正弦函数公式,二倍角的余弦函数公式,正弦函数的单调性,同角三角函数间的基本关系,以及三角形的边角关系,熟练掌握定理及公式是解本题的关键。
(1)(1)由两向量的坐标,利用平面向量的数量积运算法则列出关系式,再利用两角和与差的直正弦函数公式及二倍角的余弦函数公式化简,整理后得到一个角的正弦函数,找出ω的值,代入周期公式,即可求出函数的最小正周期;根据正弦函数的单调递减区间列出关于x的不等式,求出不等式的解集即可得到函数的递减区间;
(2)由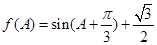
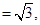 ,
,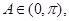 得
得 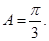
由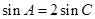 得
得 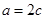 .又
.又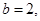 结合余弦定理得到结论。
结合余弦定理得到结论。
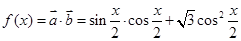
=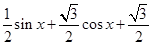
=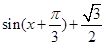

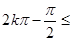 x+
x+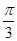
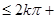
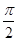 ……即2k
……即2k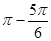
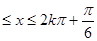 ……
……
所以…函数的单调递增区间是[2k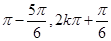 ],
],
周期T=2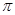 6分
6分
(Ⅱ)由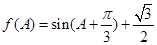
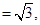 ,
,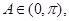 得
得 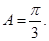
由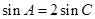 得
得 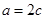 .又
.又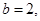
由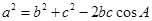 得
得 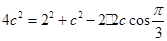
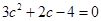 ,
,
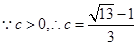 …………………………12分
…………………………12分


科目:高中数学 来源: 题型:
| 1 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| m |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com