
思路分析:根据复数与复平面上点的对应关系,知复数z对应的点在第几象限与复数z的实部和虚部有关.所以本题的关键是判断(a2-2a+4)与-(a2-2a+2)的符号.求复数z对应点的轨迹问题,首先把z表示成z=x+yi(x,y∈R)的形式,然后寻求x、y之间的关系,但要注意参数限定的条件.
解:由a2-2a+4=(a-1)2+3≥3,-(a2-2a+2)=-(a-1)2-1≤-1,
得z的实部为正数,z的虚部为负数.
∴复数z的对应点在第四象限.
设z=x+yi(x,y∈R),则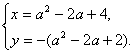
消去a2-2a,得y=-x+2(x≥3).∴复数z的对应点的轨迹是一条直线,其方程为y=-x+2(x≥3).


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com