
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点A为椭圆的右顶点,点B为椭圆的上顶点,点F为椭圆的左焦点,且
,点A为椭圆的右顶点,点B为椭圆的上顶点,点F为椭圆的左焦点,且![]() 的面积是
的面积是![]() .
.
Ⅰ.求椭圆C的方程;
Ⅱ.设直线![]() 与椭圆C交于P、Q两点,点P关于x轴的对称点为
与椭圆C交于P、Q两点,点P关于x轴的对称点为![]() (
(![]() 与
与![]() 不重合),则直线
不重合),则直线![]() 与x轴交于点H,求
与x轴交于点H,求![]() 面积的取值范围.
面积的取值范围.
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:
【题目】某中学图书馆举行高中志愿者检索图书的比赛,从高一、高二两个年级各抽取10名志愿者参赛。在规定时间内,他们检索到的图书册数的茎叶图如图所示,规定册数不小于20的为优秀.
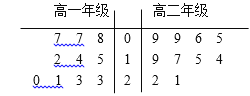
(Ⅰ) 从两个年级的参赛志愿者中各抽取两人,求抽取的4人中至少一人优秀的概率;
(Ⅱ) 从高一10名志愿者中抽取一人,高二10名志愿者中抽取两人,3人中优秀人数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
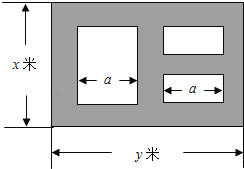
【题目】某市近郊有一块大约![]() 的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为
的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为![]() 平方米.
平方米.
(1)分别用![]() 表示
表示![]() 和
和![]() 的函数关系式,并给出定义域;
的函数关系式,并给出定义域;
(2)怎样设计能使![]() 取得最大值,并求出最大值.
取得最大值,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】茎叶图记录了甲,乙两组各四名同学单位时间内引体向上的次数,乙组记录中有一个数据模糊,无法确认,在图中以X表示.
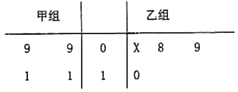
(1)如果X=8,求乙组同学单位时间内引体向上次数的平均数和方差;
(2)如果X=9,分别从甲,乙两组中随机选取一名同学,求这两名同学单位时间内引体向上次数和为19的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() ,x∈R.
,x∈R.
(1)若f(x)是偶函数,求实数a的值;
(2)当a>0时,不等式f(sinx![]() cosx)﹣f(4+t)≥0对任意的x∈
cosx)﹣f(4+t)≥0对任意的x∈![]() 恒成立,求实数t的取值范围;
恒成立,求实数t的取值范围;
(3)当a>0时,关于x的方程![]() 在区间[1,2]上恰有两个不同的实数解,求实数a的取值范围.
在区间[1,2]上恰有两个不同的实数解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 中,
中,![]() ,且
,且![]() ,其前
,其前![]() 项和为
项和为![]() ,且
,且![]() 为等比数列.
为等比数列.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若![]() ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() .设
.设![]() 是整数,问是否存在正整数
是整数,问是否存在正整数![]() ,使等式
,使等式![]() 成立?若存在,求出
成立?若存在,求出![]() 和相应的
和相应的![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com