
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 由已知可得πcos x∈[-π,π],若sin(πcos x)=0,则πcos x=-π,πcos x=π或πcos x=0,分别求满足条件的x值的个数,最后综合讨论结果,可得答案.
解答 解:当x∈[0,2π]时,
cos x∈[-1,1],
πcos x∈[-π,π],
当πcos x=-π,即cosx=-1,即x=π时,sin(πcos x)=0,
当πcos x=π,即cosx=1,即x=0,或2π时,sin(πcos x)=0,
当πcos x=0,即cosx=0,即,即x=$\frac{1}{2}$π,或x=$\frac{3}{2}$π时,sin(πcos x)=0,
综上所述,函数f(x)=sin(πcos x)在区间[0,2π]上有5零点.
故选:C
点评 本题主要考查了函数零点的意义和判断方法,三角函数的图象和性质,分类讨论思想,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
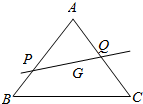 如图,设G为△ABC的重心,过G的直线l分别交AB,AC于P,Q,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$,$\overrightarrow{AQ}$=n$\overrightarrow{AC}$,令$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$
如图,设G为△ABC的重心,过G的直线l分别交AB,AC于P,Q,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$,$\overrightarrow{AQ}$=n$\overrightarrow{AC}$,令$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | 频数 | 频率 |
| [65,70] | 3 | 0.12 |
| (70,75] | 5 | 0.20 |
| (75,80] | n | x |
| (80,85] | 7 | y |
| (85,90] | m | 0.08 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,2015) | B. | (1,2015) | C. | (2,2014) | D. | (1,2014) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com