练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，有一个水平放置的透明无盖的正方体容器，容器高8cm，将一个球放在容器口，再向容器注水，当球面恰好接触水面时测得水深为6cm，如不计容器的厚度，则球的体积为（ ）

    A.
    B.
    C.
    D.

    【答案】A
    【解析】解：设正方体上底面所在平面截球得小圆M，
    则圆心M为正方体上底面正方形的中心．如图．
    设球的半径为R，根据题意得球心到上底面的距离等于（R﹣2）cm，
    而圆M的半径为4，由球的截面圆性质，得R2=（R﹣2）2+42 ，
    解出R=5，
    ∴根据球的体积公式，该球的体积V= = = ．
    故选A．

    设正方体上底面所在平面截球得小圆M，可得圆心M为正方体上底面正方形的中心．设球的半径为R，根据题意得球心到上底面的距离等于（R﹣2）cm，而圆M的半径为4，由球的截面圆性质建立关于R的方程并解出R=5，用球的体积公式即可算出该球的体积．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面为平行四边形， ， ，且底面.

    （1）证明：平面平面；

    （2）若为的中点，且，求二面角的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2015年推出一种新型家用轿车，购买时费用为16.9万元，每年应交付保险费、养路费及汽油费共1.2万元，汽车的维修费为：第一年无维修费用，第二年为0.2万元，从第三年起，每年的维修费均比上一年增加0.2万元.

    （I）设该辆轿车使用n年的总费用（包括购买费用、保险费、养路费、汽油费及维修费）为f(n)，求f(n)的表达式；

    （II）这种汽车使用多少报废最合算（即该车使用多少年，年平均费用最少）？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知圆的方程为，点的坐标为.

    （1）求过点且与圆相切的直线方程；

    （2）过点任作一条直线与圆交于不同两点，，且圆交轴正半轴于点，求证：直线与的斜率之和为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某商店为了解气温对某产品销售量的影响，随机记录了该商店月份中天的日销售量（单位：千克）与该地当日最低气温（单位：℃）的数据，如表所示：

    （1）求与的回归方程：

    （2）判断与之间是正相关还是负相关；若该地月份某天的最低气温为，请用（1）中的回归方程预测该商店当日的销售量．

    参考公式：，．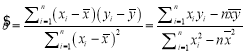

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，三角形所在的平面与长方形所在的平面垂直，.点是边的中点，点分别在线段，上，且.

    (1)证明：；

    (2)求二面角的正切值；

    (3)求直线与直线PG所成角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）若不等式的解集为，求实数的值；

    （2）若不等式对一切实数恒成立，求实数的取值范围；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知⊙的半径为，圆心的坐标为，其中．，为该圆的两条切线，为坐标原点，，为切点，在第一象限，在第四象限．

    （）若时，求切线，的斜率．

    （）若时，求外接圆的标准方程．

    （）当点在轴上运动时，将表示成的函数，并求函数的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列满足，若为单调递增的等差数列，其前项和为，则__________；若为单调递减的等比数列，其前项和为，则__________.

    查看答案和解析>>

    同步练习册答案