
【题目】2015年推出一种新型家用轿车,购买时费用为16.9万元,每年应交付保险费、养路费及汽油费共1.2万元,汽车的维修费为:第一年无维修费用,第二年为0.2万元,从第三年起,每年的维修费均比上一年增加0.2万元.
(I)设该辆轿车使用n年的总费用(包括购买费用、保险费、养路费、汽油费及维修费)为f(n),求f(n)的表达式;
(II)这种汽车使用多少报废最合算(即该车使用多少年,年平均费用最少)?
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,则异面直线AE与BF所成角的余弦值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆C: ![]() 经过点P(1,
经过点P(1, ![]() ),离心率e=
),离心率e= ![]() ,直线l的方程为x=4.
,直线l的方程为x=4. 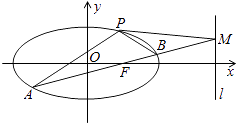
(1)求椭圆C的方程;
(2)AB是经过右焦点F的任一弦(不经过点P),设直线AB与直线l相交于点M,记PA,PB,PM的斜率分别为k1 , k2 , k3 . 问:是否存在常数λ,使得k1+k2=λk3?若存在,求λ的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法的错误的是( )
A. 经过定点![]() 的倾斜角不为
的倾斜角不为![]() 的直线的方程都可以表示为
的直线的方程都可以表示为![]()
B. 经过定点![]() 的倾斜角不为
的倾斜角不为![]() 的直线的方程都可以表示为
的直线的方程都可以表示为![]()
C. 不经过原点的直线的方程都可以表示为![]()
D. 经过任意两个不同的点![]() 、
、![]() 直线的方程都可以表示为
直线的方程都可以表示为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器注水,当球面恰好接触水面时测得水深为6cm,如不计容器的厚度,则球的体积为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了检验设备M与设备N的生产效率,研究人员作出统计,得到如下表所示的结果,则
设备M | 设备N | |
生产出的合格产品 | 48 | 43 |
生产出的不合格产品 | 2 | 7 |
附:
P(K2≥k0) | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
参考公式:![]() ,其中
,其中![]() .
.
A. 有90%的把握认为生产的产品质量与设备的选择有关
B. 没有90%的把握认为生产的产品质量与设备的选择有关
C. 可以在犯错误的概率不超过0.01的前提下认为生产的产品质量与设备的选择有关
D. 不能在犯错误的概率不超过0.1的前提下认为生产的产品质量与设备的选择有关
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com