
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,圆
中,圆![]() :
:![]() ,直线
,直线![]() :
:![]() ,直线
,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() ,以原点
,以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)写出直线![]() 与圆
与圆![]() 的交点极坐标及直线
的交点极坐标及直线![]() 的参数方程;
的参数方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
【题目】已知平面内一动点![]() (
(![]() )到点
)到点![]() 的距离与点
的距离与点![]() 到
到![]() 轴的距离的差等于1,
轴的距离的差等于1,
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与轨迹
与轨迹![]() 相交于不同于坐标原点
相交于不同于坐标原点![]() 的两点
的两点![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年,某地认真贯彻落实中央十九大精神和各项宏观调控政策,经济运行平稳增长,民生保障持续加强,惠民富民成效显著,城镇居民收入稳步增长,收入结构稳中趋优.据当地统计局公布的数据,现将8月份至12月份当地的人均月收入增长率如图(一)与人均月收入绘制成如图(二)所示的不完整的条形统计图.现给出如下信息:
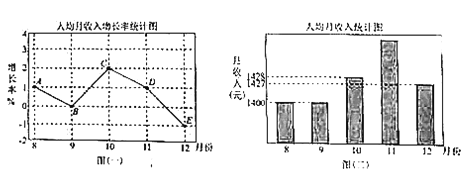
①10月份人均月收入增长率为![]() ;
;
②11月份人均月收入约为1442元;
③12月份人均月收入有所下降;
④从上图可知该地9月份至12月份这四个月与8月份相比人均月收入均得到提高.
其中正确的信息个数为( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,左顶点为
,左顶点为![]() .过点
.过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程:
的方程:
(2)已知![]() 为
为![]() 的中点,是否存在定点
的中点,是否存在定点![]() ,对任意的直线
,对任意的直线![]() ,
,![]() 恒成立?若存在,求出点
恒成立?若存在,求出点![]() 的坐标;若不存在说明理由;
的坐标;若不存在说明理由;
(3)过![]() 点作直线
点作直线![]() 的平行线与椭圆
的平行线与椭圆![]() 相交,
相交,![]() 为其中一个交点,求
为其中一个交点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关平面向量分解定理的四个命题:
(1)一个平面内有且只有一对不平行的向量可作为表示该平面所有向量的基;
(2)一个平面内有无数多对不平行向量可作为表示该平面内所有向量的基;
(3)平面向量的基向量可能互相垂直;
(4)一个平面内任一非零向量都可唯一地表示成该平面内三个互不平行向量的线性组合.
其中正确命题的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知城市![]() 周边有两个小镇
周边有两个小镇![]() 、
、![]() ,其中乡镇
,其中乡镇![]() 位于城市
位于城市![]() 的正东方
的正东方![]() 处,乡镇
处,乡镇![]() 与城市
与城市![]() 相距
相距![]() ,
,![]() 与
与![]() 夹角的正切值为2,为方便交通,现准备建设一条经过城市
夹角的正切值为2,为方便交通,现准备建设一条经过城市![]() 的公路
的公路![]() ,使乡镇
,使乡镇![]() 和
和![]() 分别位于
分别位于![]() 的两侧,过
的两侧,过![]() 和
和![]() 建设两条垂直
建设两条垂直![]() 的公路
的公路![]() 和
和![]() ,分别与公路
,分别与公路![]() 交汇于
交汇于![]() 、
、![]() 两点,以
两点,以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,建立如图所示的平面直角坐标系
轴,建立如图所示的平面直角坐标系![]() .
.
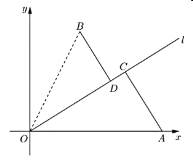
(1)当两个交汇点![]() 、
、![]() 重合,试确定此时
重合,试确定此时![]() 路段长度;
路段长度;
(2)当![]() ,计算此时两个交汇点
,计算此时两个交汇点![]() 、
、![]() 到城市
到城市![]() 的距离之比;
的距离之比;
(3)若要求两个交汇点![]() 、
、![]() 的距离不超过
的距离不超过![]() ,求
,求![]() 正切值的取值范围.
正切值的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() ,
,![]() 是抛物线上的两个动点,且
是抛物线上的两个动点,且![]() ,过
,过![]() ,
,![]() 两点分别作抛物线的切线,设其交点为
两点分别作抛物线的切线,设其交点为![]() .
.
(1)若直线![]() 与
与![]() ,
,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,且
,且![]() 的面积为
的面积为![]() ,求
,求![]() 的值;
的值;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大以来,某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求,带领广大农村地区人民群众脱贫奔小康。经过不懈的奋力拼搏,新农村建设取得巨大进步,农民年收入也逐年增加。为了更好的制定2019年关于加快提升农民年收人力争早日脱贫的工作计划,该地扶贫办统计了2018年50位农民的年收人并制成如下频率分布直方图:
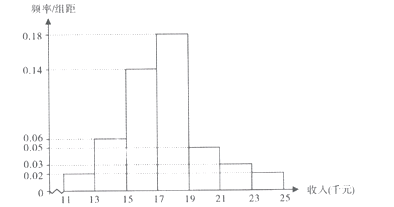
(1)根据频率分布直方图,估计50位农民的年平均收入![]() (单位:千元)(同一组数据用该组数据区间的中点值表示);
(单位:千元)(同一组数据用该组数据区间的中点值表示);
(2)由频率分布直方图,可以认为该贫困地区农民年收入![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为年平均收入
近似为年平均收入![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经计算得
,经计算得![]() .利用该正态分布,求:
.利用该正态分布,求:
(i)在2019年脱贫攻坚工作中,若使该地区约有占总农民人数的![]() 的农民的年收入高于扶贫办制定的最低年收入标准,则最低年收入大约为多少千元?
的农民的年收入高于扶贫办制定的最低年收入标准,则最低年收入大约为多少千元?
(ii)为了调研“精准扶贫,不落一人”的政策要求落实情况, 扶贫办随机走访了1000位农民。若每个农民的年收人相互独立,问:这1000位农民中的年收入不少于12.14千元的人数最有可能是多少?
附:参考数据与公式![]() ,若
,若![]() ~
~![]() ,则①
,则①![]() ;②
;②![]() ;③
;③![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com