
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,抛物线上横坐标为
,抛物线上横坐标为![]() 的点到抛物线顶点的距离与该点到抛物线准线的距离相等。
的点到抛物线顶点的距离与该点到抛物线准线的距离相等。
(1)求抛物线![]() 的方程;
的方程;
(2)设直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,若
两点,若![]() ,求实数
,求实数![]() 的值。
的值。
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学成就的杰出代表,其中《方田》章有弧田面积计算问题,计算术曰:以弦乘矢,矢又自乘,并之,二而一.其大意是,弧田面积计算公
式为:弧田面积=![]() ,弧田是由圆弧(简称为弧田弧)和以圆
,弧田是由圆弧(简称为弧田弧)和以圆
弧的两端为顶点的线段(简称为弧田弦)围成的平面图形,公式中“弦”指的是弧
田弦的长,“矢”等于弧田弧所在圆的半径与圆心到弧田弦的距离之差.现有一弧
田,其弦长AB等于6米,其弧所在圆为圆O,若用上述弧田面积计算公式算得该
弧田的面积为![]() 平方米,则cos∠AOB= ( )
平方米,则cos∠AOB= ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王、小李两位同学玩掷骰子(骰子质地均匀)游戏,规则:小王先掷一枚骰子,向上的点数记为![]() ;小李后掷一枚骰子,向上的点数记为
;小李后掷一枚骰子,向上的点数记为![]() .
.
(1)求![]() 能被
能被![]() 整除的概率.
整除的概率.
(2)规定:若![]() ,则小王赢;若
,则小王赢;若![]() ,则小李赢,其他情况不分输赢.试问这个游戏规则公平吗?请说明理由.
,则小李赢,其他情况不分输赢.试问这个游戏规则公平吗?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知x0,x0+![]() 是函数f(x)=cos2(wx﹣
是函数f(x)=cos2(wx﹣![]() )﹣sin2wx(ω>0)的两个相邻的零点
)﹣sin2wx(ω>0)的两个相邻的零点
(1)求![]() 的值;
的值;
(2)若对任意![]() ,都有f(x)﹣m≤0,求实数m的取值范围.
,都有f(x)﹣m≤0,求实数m的取值范围.
(3)若关于![]() 的方程
的方程![]() 在
在![]() 上有两个不同的解,求实数
上有两个不同的解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂修建一个长方体无盖蓄水池,其容积为6400立方米,深度为4米.池底每平方米的造价为120元,池壁每平方米的造价为100元.设池底长方形的长为x米.
(Ⅰ)求底面积,并用含x的表达式表示池壁面积;
(Ⅱ)怎样设计水池能使总造价最低?最低造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点P是单位圆上的动点,过点P作x轴的垂线与射线y=![]() x(x≥0)交于点Q,与x轴交于点M.记∠MOP=α,且α∈(﹣
x(x≥0)交于点Q,与x轴交于点M.记∠MOP=α,且α∈(﹣![]() ,
, ![]() ).
).
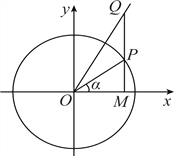
(Ⅰ)若sinα=![]() ,求cos∠POQ;
,求cos∠POQ;
(Ⅱ)求△OPQ面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
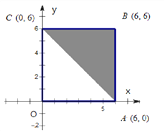
【题目】如图:区域A是正方形OABC(含边界),区域B是三角形ABC(含边界)。
(Ⅰ)向区域A随机抛掷一粒黄豆,求黄豆落在区域B的概率;
(Ⅱ)若x,y分别表示甲、乙两人各掷一次骰子所得的点数,求点(x,y)落在区域B的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两厂产品的质量,从两厂生产的产品中分别随机抽取各10件样品,测量产品中某种元素的含量(单位:毫克),如图是测量数据的茎叶图:
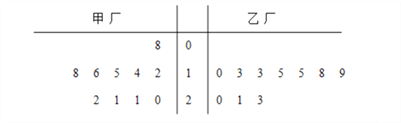
规定:当产品中的此种元素含量不小于16毫克时,该产品为优等品.
(1)从乙厂抽出的上述10件样品中,随机抽取3件,求抽到的3件样品中优等品数![]() 的分布列及其数学期望
的分布列及其数学期望![]() ;
;
(2)从甲厂的10件样品中有放回地逐个随机抽取3件,也从乙厂的10件样品中有放回地逐个随机抽取3件,求抽到的优等品数甲厂恰比乙厂多2件的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com