练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．已知φ∈（0，π），若函数f（x）=cos（2x+φ）为奇函数，则φ=$\frac{π}{2}$．

    分析 根据余弦函数的图象和性质即可得到结论．

    解答 解：若函数f（x）=cos（2x+φ）为奇函数，
    则φ=$\frac{π}{2}$+kπ，k∈Z，
    又φ∈（0，π），
    所以φ=$\frac{π}{2}$．
    故答案为：$\frac{π}{2}$．

    点评 本题主要考查了余弦函数的奇偶性问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    14．将函数f（x）=$\sqrt{3}$sinxcosx+sin2x的图象上各点的纵坐标不变，横坐标变为原来的2倍，再沿x轴向右平移$\frac{π}{6}$个单位，得到函数y=g（x）的图象，则y=g（x）的一个递增区间是（　　）
    A．$[{-\frac{π}{6}，\frac{5π}{6}}]$B．$[{-\frac{π}{2}，\frac{π}{2}}]$C．$[{-\frac{π}{12}，\frac{4π}{3}}]$D．$[{-\frac{π}{4}，0}]$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知平面区域D=$\left\{{（{x，y}）\left|\begin{array}{l}\\ 3x+y≥3\\ x-y≤2\\ x+3y≤3\end{array}\right.}\right\}$，z=3x-2y，若命题“?（x0，y0）∈D，z＞m”为假命题，则实数m的最小值为$\frac{25}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．等边三角形ABC与正方形ABDE有一公共边AB，二面角C-AB-D的余弦值为$\frac{\sqrt{3}}{3}$，M，N分别是AC．BC的中点，则EM，AN所成角的余弦值等于（　　）
    A．$\frac{1}{3}$B．$\frac{\sqrt{3}}{3}$C．$\frac{\sqrt{6}}{3}$D．$\frac{1}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，下列说法正确的是（　　）
    A．f（x）的图象关于直线x=-$\frac{2π}{3}$对称
    B．函数f（x）在[-$\frac{π}{3}$，0]上单调递增
    C．f（x）的图象关于点（-$\frac{5π}{12}$，0）对称
    D．将函数y=2sin（2x-$\frac{π}{6}$）的图象向左平移$\frac{π}{6}$个单位得到f（x）的图象

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知P（x0，y0）是单位圆上任一点，将射线OP绕点O顺时针转$\frac{π}{3}$到OQ交单位圆与点Q（x1，y1），若my0-y1的最大值为$\frac{3}{2}$，则实数m=$\frac{1±\sqrt{6}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

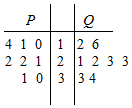    16．从某工厂生产的P，Q两种型号的玻璃种分别随机抽取8个样品进行检查，对其硬度系数进行统计，统计数据用茎叶图表示（如图所示），则P组数据的众数和Q组数据的中位数分别为（　　）
    A．22和22.5B．21.5和23C．22和22D．21.5和22.5

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数f（x）=$\frac{-{3}^{x}+a}{{3}^{x+1}+b}$．
    （1）当a=b=1时，求满足f（x）=3x的x的值；
    （2）若函数f（x）是定义在R上的奇函数，
    ①判断f（x）在R的单调性并用定义法证明；
    ②当x≠0时，函数g（x）满足f（x）•[g（x）+2]=$\frac{1}{3}$（3-x-3x），若对任意x∈R且x≠0，不等式g（2x）≥m•g（x）-11恒成立，求实数m的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知：如图，空间四边形ABCD中，E，F分别是AB，AD的中点．
    求证：EF∥平面BCD．

    查看答案和解析>>

    同步练习册答案