练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在四面体SABC中,AH⊥侧面SBC,且H为△SBC的垂心,连结BH并延长交SC于点E,E到AB的距离ED=6,CD与平面AEB所成角为30°.

    （1）求证:SC⊥AB;

    （2）求EC的长.

    (1)证明:∵H为△SBC的垂心,SC⊥BE,又AH⊥平面SBC,

    ∴BE是AB在平面SBC上的射影.

    ∴SC⊥AB.

    (2)解:由(1)知,CE⊥BE,CE⊥AB,

    ∴CE⊥平面ABE.

    ∴∠CDE就是CD与平面ABE所成的角.

    ∴∠CDE=30°.在Rt△CDE中,EC=EDtan30°=23.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

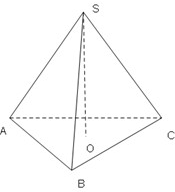    精英家教网在直角△ABC中，两直角边的长分别为a，b，直角顶点C到斜边的距离为h，则易证
    1
    h2
    =
    1
    a2
    +
    1
    b2
    ．在四面体SABC中，侧棱SA，SB，SC两两垂直，SA=a，SB=b，SC=c，点S到平面ABC的距离为h，类比上述结论，写出h与a，b，c的等式关系并证明．

    查看答案和解析>>

    科目：高中数学 来源：江苏省滨海中学高二年级第二学期阶段考试数学试卷苏教版 苏教版 题型：044

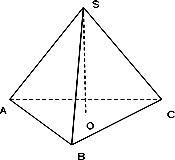
    (文科)在直角△ABC中，两直角边的长分别为a，b，直角顶点C到斜边的距离为h，则易证．在四面体SABC中，侧棱SA，SB，SC两两垂直，SA＝a，SB＝，SC＝c，点S到平面ABC的距离为h，类比上述结论，写出h与a，b，c的等式关系并证明．

    查看答案和解析>>

    科目：高中数学 来源：2007-2008学年江苏省泰州市高二（下）期末数学试卷（文科）（解析版） 题型：解答题

    在直角△ABC中，两直角边的长分别为a，b，直角顶点C到斜边的距离为h，则易证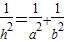．在四面体SABC中，侧棱SA，SB，SC两两垂直，SA=a，SB=b，SC=c，点S到平面ABC的距离为h，类比上述结论，写出h与a，b，c的等式关系并证明．

    查看答案和解析>>

    科目：高中数学 来源：2011年江苏宿迁市洪祥中学高三数学课堂作业设计9-12（解析版） 题型：解答题

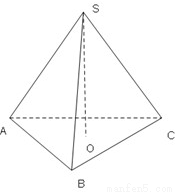    在直角△ABC中，两直角边的长分别为a，b，直角顶点C到斜边的距离为h，则易证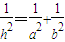．在四面体SABC中，侧棱SA，SB，SC两两垂直，SA=a，SB=b，SC=c，点S到平面ABC的距离为h，类比上述结论，写出h与a，b，c的等式关系并证明．

    查看答案和解析>>

    同步练习册答案