分析:(I)由题意建立如图的空间直角坐标系,写出相应点的坐标,利用两平面的法向量的夹角与两半平面夹角之间的关系求出二面角的大小;
(II)因为E,F分别是棱BB1,AD中点,利用条件得到四边形BED1F为平行四边形,进而得到BG∥平面AD1E,GF∥平面AD1E,再利用线面平行的判定定理证出所求.
解答: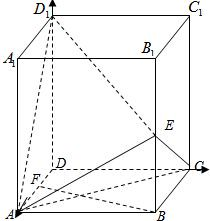
解:(Ⅰ)以D为坐标原点,DA、DC、DD
1分别为X、Y、Z轴建立空间直角坐标系如图.
则相应点的坐标分别为D
1(0,0,2),A(1,0,0),C(0,1,0),E(1,1,1),
∴
=(0,0,2)-(1,1,1)=(-1,-1,1)=(1,1,1)-(1,0,0)=(0,1,1),
=(0,1,0)-(1,0,0)=(-1,1,0)设平面AED
1、平面AEC的法向量分别为
=(a,b,1),=(c,d,1),
由
??,
由
??,
∴
=(2,-1,1),=(-1,-1,1),
∴
cos<,>===0∴二面角D
1-AE-C的大小为90°.
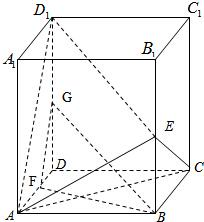
(Ⅱ)证明:取DD
1的中点G,连接GB,GF
∵E,F分别是棱BB
1,AD中点
∴GF∥AD
1,BE∥D
1G且BE=D
1G,
∴四边形BED
1F为平行四边形,∴D
1E∥BF
又D
1E,D
1A?平面AD
1E,BG,GF?平面AD
1E
∴BG∥平面AD
1E,GF∥平面AD
1E
∵GF,GB⊆平面BGF,∴平面BGF∥平面AD
1E
∵BF⊆平面AD
1E,∴直线BF∥平面AD
1E
点评:此题重点考查了建立空间直角坐标系,利用平面的法向量的夹角与二面角的大小之间的关系,求解出二面角的大小,还考查了利用线线平行证明线面平行和面面平行,进而利用面面平行的性质定理得线面平行.

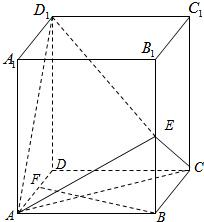 在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、F分别是棱B1B、DA的中点.
在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、F分别是棱B1B、DA的中点. 解:(Ⅰ)以D为坐标原点,DA、DC、DD1分别为X、Y、Z轴建立空间直角坐标系如图.
解:(Ⅰ)以D为坐标原点,DA、DC、DD1分别为X、Y、Z轴建立空间直角坐标系如图. (Ⅱ)证明:取DD1的中点G,连接GB,GF
(Ⅱ)证明:取DD1的中点G,连接GB,GF

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案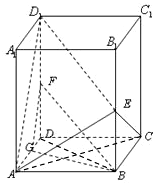 在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、G、F分别是棱B1B、D1D、DA的中点.
在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、G、F分别是棱B1B、D1D、DA的中点.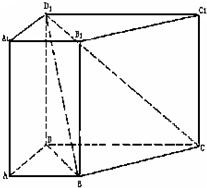 在直四棱柱ABCD-A1B1C1D1中,已知AB∥CD,AB=AD=1,D1D=CD=2,AB⊥AD.
在直四棱柱ABCD-A1B1C1D1中,已知AB∥CD,AB=AD=1,D1D=CD=2,AB⊥AD.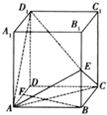 在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、F分别是棱B1B、DA的中点.
在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、F分别是棱B1B、DA的中点. 如图,在直四棱柱ABCD-A1B1C1D1中,点E,F分别在AA1,CC1上,且AE=
如图,在直四棱柱ABCD-A1B1C1D1中,点E,F分别在AA1,CC1上,且AE= 在直四棱柱ABCD-A1B1C1D1中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,AB=AD=1,CD=CC1=2,E为棱AA1的中点,F为棱BB1上的动点.
在直四棱柱ABCD-A1B1C1D1中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,AB=AD=1,CD=CC1=2,E为棱AA1的中点,F为棱BB1上的动点.