
 ,函数
,函数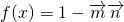
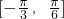 上的值域.
上的值域.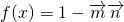 =1-(2cos2x-2
=1-(2cos2x-2 sinxcosx)=1-(1+cos2x-
sinxcosx)=1-(1+cos2x- sin2x)=
sin2x)=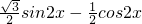 )=2sin(2x-
)=2sin(2x- ),
), =π.
=π.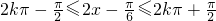 ,k∈z,可得
,k∈z,可得 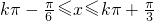 ,k∈z,
,k∈z,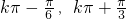 ],k∈z.
],k∈z.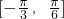 ,∴2x-
,∴2x- ∈
∈ ,故-1≤sin(2x-
,故-1≤sin(2x- )≤
)≤ ,-2≤2sin(2x-
,-2≤2sin(2x- )≤1,
)≤1,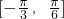 上的值域为[-2,1].
上的值域为[-2,1]. ),求出最小正周期,再由
),求出最小正周期,再由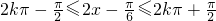 ,k∈z,求出x的范围,即可求得单调递增区间.
,k∈z,求出x的范围,即可求得单调递增区间.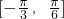 ,可得 2x-
,可得 2x- ∈
∈ ,从而求得2sin(2x-
,从而求得2sin(2x- )的范围,即可求得值域.
)的范围,即可求得值域.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届宁夏高一下学期期中考试数学试卷(解析版) 题型:解答题
已知向量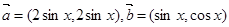 ,函数
,函数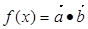 .
.
(1)求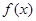 的单调区间;
的单调区间;
(2)请说出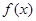 的图象是由
的图象是由 的图象经过怎样的变换得到的(说清每一步的变换方法);
的图象经过怎样的变换得到的(说清每一步的变换方法);
(3)当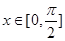 时,求
时,求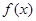 的最大值及取得最大值时的
的最大值及取得最大值时的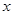 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年天津市高三第四次月考理科数学试卷(解析版) 题型:解答题
已知向量 ,函数
,函数 ·
·
(1)求函数 的最小正周期T及单调减区间
的最小正周期T及单调减区间
(2)已知 分别是△ABC内角A,B,C的对边,其中A为锐角,
分别是△ABC内角A,B,C的对边,其中A为锐角, 且
且
 ,求A,b和△ABC的面积S
,求A,b和△ABC的面积S
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南省高三第三次考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知向量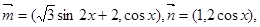 设函数
设函数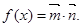
(1)求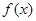 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;
(2)在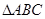 中
中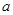 、
、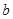 、
、 分别是角
分别是角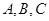 的对边,若
的对边,若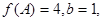
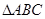 的面积为
的面积为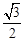 ,求
,求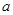 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014届山西省高一下学期期中理科数学试卷(解析版) 题型:解答题
已知向量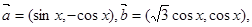 设函数
设函数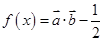 ;
;
(1)写出函数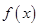 的单调递增区间;
的单调递增区间;
(2)若x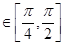 求函数
求函数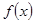 的最值及对应的x的值;
的最值及对应的x的值;
(3)若不等式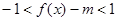 在x
在x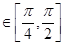 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届山西大学附中高一第二学期期中考试数学试卷(解析版) 题型:解答题
已知向量 ,函数
,函数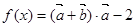
(1)求函数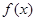 的最小正周期
的最小正周期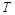 ;
;
(2)将函数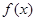 的图像向左平移
的图像向左平移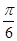 上个单位后,再将所得图像上所有点的横坐标伸长为原来的3倍,得到函数
上个单位后,再将所得图像上所有点的横坐标伸长为原来的3倍,得到函数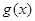 的图像,求函数
的图像,求函数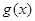 的解析式及其对称中心坐标
的解析式及其对称中心坐标
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com