
已知抛物线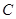 的顶点为原点,其焦点
的顶点为原点,其焦点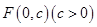 到直线
到直线 的距离为
的距离为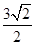 .设
.设 为直线
为直线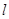 上的点,过点
上的点,过点 作抛物线
作抛物线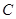 的两条切线
的两条切线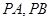 ,其中
,其中 为切点.
为切点.
(Ⅰ)求抛物线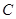 的方程;
的方程;
(Ⅱ)设点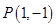 为直线
为直线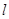 上的点,求直线
上的点,求直线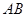 的方程;
的方程;
(Ⅲ) 当点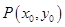 在直线
在直线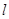 上移动时,求
上移动时,求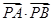 的最小值.
的最小值.
(1) 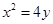 (2)
(2)
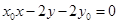 (3)
(3)

【解析】
试题分析: (1)利用点到直线的距离公式直接求解C的值,便可确定抛物线方程;(2)利用求导的思路确定抛物线的两条切线,借助均过点P,得到直线方程;(3)通过直线与抛物线联立,借助韦达定理将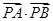 进行转化处理,通过参数的消减得到函数关系式
进行转化处理,通过参数的消减得到函数关系式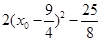 是解题的关键,然后利用二次函数求最值,需注意变量的范围.
是解题的关键,然后利用二次函数求最值,需注意变量的范围.
试题解析:(1)依题意 ,解得
,解得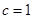 (负根舍去) (2分)
(负根舍去) (2分)
 抛物线
抛物线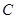 的方程为
的方程为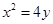 ;
(4分)
;
(4分)
(2)设点 ,
,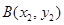 ,由
,由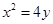 ,即
,即 得
得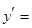
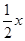 .
.
∴抛物线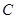 在点
在点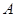 处的切线
处的切线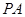 的方程为
的方程为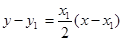 ,即
,即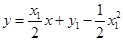 .
(5分)
.
(5分)
因为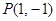 在切线
在切线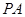 上且
上且 所以
所以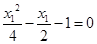 ,
,
从而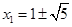 同理,
同理,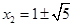 , (6分)
, (6分)
不妨取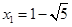 ,
,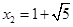 所以
所以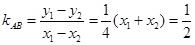 , (7分)
, (7分)
又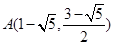 ,∴直线
,∴直线 的方程为
的方程为  (8分)
(8分)
(3)依据(2)由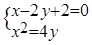 得,
得, (9分)
(9分)
于是 ,
(10分)
,
(10分)
所以
又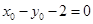 ,所以
,所以 , (11分)
, (11分)
从而 (12分)
(12分)
考点:抛物线的方程、定义、切线方程以及直线与抛物线的位置关系.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:天骄之路中学系列 读想用 高二数学(上) 题型:044
已知抛物线C的对称轴与y轴平行,顶点到原点的距离为5,若将抛物线C向上平移3个单位,则在x轴上截得的线段为原抛物线C在x轴上截得的线段的一半;若将抛物线C向左平移1个单位,则所得抛物线过原点,求抛物线C的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com