
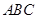 三个内角分别为
三个内角分别为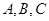 向量
向量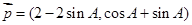 与向量
与向量 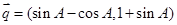 是共线向量.
是共线向量.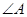 的值;
的值;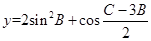 的值域.
的值域.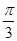 . (2)y∈
. (2)y∈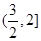
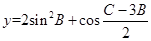 的值域需将函数化为一角一名称的形式,y=sin(2B-
的值域需将函数化为一角一名称的形式,y=sin(2B- )+1.再用整体法,得出整体角的范围∴2B-
)+1.再用整体法,得出整体角的范围∴2B- ∈(
∈( ,
,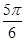 ).
).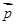 ,
,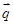 共线,
共线,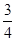 . ………3分
. ………3分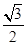 ,∴A=
,∴A=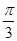 . …………5分
. …………5分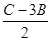 =2sin2B+cos
=2sin2B+cos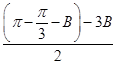 …………………6分
…………………6分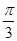 -2B)=1-cos 2B+
-2B)=1-cos 2B+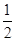 cos 2B+
cos 2B+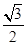 sin 2B …………8分
sin 2B …………8分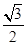 sin 2B-
sin 2B-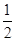 cos 2B+1=sin(2B-
cos 2B+1=sin(2B- )+1. …………10分
)+1. …………10分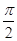 ),又因为B+A>
),又因为B+A>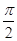 ∴
∴ <B<
<B<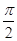 ∴2B-
∴2B- ∈(
∈( ,
,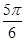 ). ……11分
). ……11分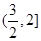


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com