
【题目】若函数 ![]() 的图象向左平移
的图象向左平移 ![]() 个单位,得到函数g(x)的图象,则下列关于g(x)叙述正确的是( )
个单位,得到函数g(x)的图象,则下列关于g(x)叙述正确的是( )
A.g(x)的最小正周期为2π
B.g(x)在 ![]() 内单调递增
内单调递增
C.g(x)的图象关于 ![]() 对称
对称
D.g(x)的图象关于 ![]() 对称
对称
【答案】C
【解析】解:函数 ![]() . 化简可得:f(x)=sin2x﹣
. 化简可得:f(x)=sin2x﹣ ![]() sinxcosx=
sinxcosx= ![]() -
- ![]() cos2x﹣
cos2x﹣ ![]() sin2x
sin2x
= ![]() ﹣sin(2x+
﹣sin(2x+ ![]() )图象向左平移
)图象向左平移 ![]() 个单位,可得:
个单位,可得: ![]() ﹣sin(2x+
﹣sin(2x+ ![]() +
+ ![]() )=
)= ![]() -sin(2x+
-sin(2x+ ![]() )=g(x)
)=g(x)
最小正周期T= ![]() ,∴A不对.
,∴A不对.
由 ![]() ≤2x+
≤2x+ ![]() ,可得:
,可得: ![]() ,g(x)在
,g(x)在 ![]() 内单调递增,∴B不对.
内单调递增,∴B不对.
由2x+ ![]() =
= ![]() ,可得x=
,可得x= ![]() ,(k∈Z),当k=0时,可得g(x)的图象的对称轴为
,(k∈Z),当k=0时,可得g(x)的图象的对称轴为 ![]() ,
,
∴C对.
由2x+ ![]() =kπ,可得x=
=kπ,可得x= ![]() ﹣
﹣ ![]() ,对称中心的横坐标为(
,对称中心的横坐标为( ![]() ,0),∴D不对.
,0),∴D不对.
故选C.
【考点精析】根据题目的已知条件,利用函数y=Asin(ωx+φ)的图象变换的相关知识可以得到问题的答案,需要掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3﹣bx2+cx+b﹣a(a>0).
(1)设c=0. ①若a=b,曲线y=f(x)在x=x0处的切线过点(1,0),求x0的值;
②若a>b,求f(x)在区间[0,1]上的最大值.
(2)设f(x)在x=x1 , x=x2两处取得极值,求证:f(x1)=x1 , f(x2)=x2不同时成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与
与![]() 轴,
轴,![]() 轴的正半轴分别交于A,B两点,原点O到直线AB的距离为
轴的正半轴分别交于A,B两点,原点O到直线AB的距离为![]() 该椭圆的离心率为
该椭圆的离心率为![]()
(1)求椭圆的方程
(2)是否存在过点P(![]() 的直线
的直线![]() 与椭圆交于M,N两个不同的点,使
与椭圆交于M,N两个不同的点,使![]() 成立?若存在,求出
成立?若存在,求出![]() 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣(a+2)x+alnx,其中常数a>0.
(Ⅰ)当a>2时,求函数f(x)的单调递增区间;
(Ⅱ)设定义在D上的函数y=h(x)在点P(x0 , h(x0))处的切线方程为l:y=g(x),若 ![]() >0在D内恒成立,则称P为函数y=h(x)的“类对称点”.当a=4时,试问y=f(x)是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
>0在D内恒成立,则称P为函数y=h(x)的“类对称点”.当a=4时,试问y=f(x)是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月15日中的某一天到达该市,并停留2天.
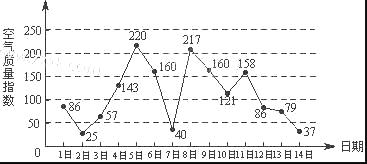
(Ⅰ)求此人到达当日空气质量优良的概率;
(Ⅱ)求此人在该市停留期间只有1天空气重度污染的概率;
(Ⅲ)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+bx﹣c,f(x)在点(1,f(1))处的切线方程为x+y+4=0.
(1)求f(x)的解析式;
(2)求f(x)的单调区间;
(3)若在区间 ![]() 内,恒有f(x)≥2lnx+kx成立,求k的取值范围.
内,恒有f(x)≥2lnx+kx成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}.满足:an+1>an(n∈N*),a1=1,该数列的前三项分别加上1,1,3后成等比数列,an+2log2bn=﹣1.
(Ⅰ)分别求数列{an},{bn}的通项公式;
(Ⅱ)求数列{anbn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP= ![]() .
. 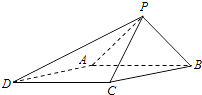
(1)求证:AB⊥PC;
(2)求二面角B一PC﹣D的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com