
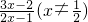 .
. )+F(
)+F( )+…+F(
)+…+F( );
); }为等差数列(n∈N*),并求数列{an}的通项公式;
}为等差数列(n∈N*),并求数列{an}的通项公式;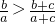 ,利用此结论,求证:a1a2…an>
,利用此结论,求证:a1a2…an> (n∈N*).
(n∈N*).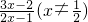 ,
,
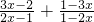 =
=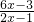 =3,
=3, )+F(
)+F( )+…+F(
)+…+F( ),①
),① )+F(
)+F( )+…+F(
)+…+F( ),②
),② )+F(
)+F( )]+[F(
)]+[F( )+F(
)+F( )]+…+[F(
)]+…+[F( )+F(
)+F( )]=3×2010=6030,
)]=3×2010=6030, )+F(
)+F( )+…+F(
)+…+F( )=3015.
)=3015.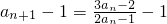 =
=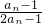 ,
,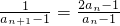 =
=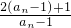 =2+
=2+ ,
,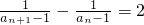 ,又
,又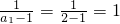 ,
, }是以2为公差,1为首项的等差数列,
}是以2为公差,1为首项的等差数列,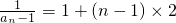 =2n-1,
=2n-1,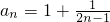 =
=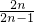 .
.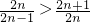 ,
,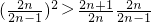 =
=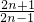 ,
,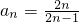 >
>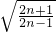 ,
,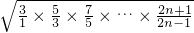 =
= (n∈N*).
(n∈N*).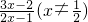 ,得F(x)+F(1-x)=3,设S=F(
,得F(x)+F(1-x)=3,设S=F( )+F(
)+F( )+…+F(
)+…+F( ),利用倒序相加法能求出F(
),利用倒序相加法能求出F( )+F(
)+F( )+…+F(
)+…+F( )的值.
)的值.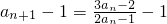 =
=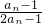 ,由此能证明证明{
,由此能证明证明{ }为等差数列(n∈N*),并求数列{an}的通项公式.
}为等差数列(n∈N*),并求数列{an}的通项公式.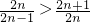 ,得
,得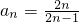 >
>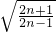 ,由此能够证明a1a2…an>
,由此能够证明a1a2…an> (n∈N*).
(n∈N*).

 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| m |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com