
(本题满分16分) 已知函数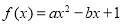 .
.
(Ⅰ)若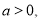 不等式
不等式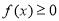 的解集为
的解集为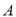 ,
,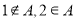 ,求
,求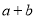 的取值范围;
的取值范围;
(Ⅱ)若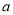 为整数,
为整数,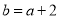 ,且函数
,且函数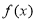 在
在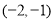 上恰有一个零点,求
上恰有一个零点,求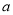 的值;
的值;
(Ⅲ)在(Ⅱ)的条件下,若函数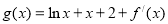 对任意的x∈
对任意的x∈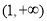 ,有
,有 恒成立,求实数
恒成立,求实数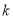 的最小值.
的最小值.
(Ⅰ)(2,+∞)(Ⅱ)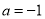 (Ⅲ)1.
(Ⅲ)1.
【解析】
试题分析:(Ⅰ))本题为线性规划求范围问题,先列出可行域:由题知 ,以a为x轴,b为y轴建立直角坐标系,由图可知直线
,以a为x轴,b为y轴建立直角坐标系,由图可知直线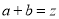 过点
过点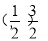 取最小值2,(Ⅱ)本题先分一次函数与二次函数讨论:
取最小值2,(Ⅱ)本题先分一次函数与二次函数讨论: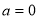 时,f(x)=-2x+1,零点为
时,f(x)=-2x+1,零点为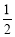 ,不合,舍去;
,不合,舍去;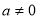 时,∵
时,∵  ∴
∴  ,
,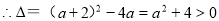 ,∴函数
,∴函数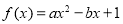 必有两个零点,再根据零点存在定理列函数
必有两个零点,再根据零点存在定理列函数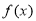 在
在 上恰有一个零点的充要条件:
上恰有一个零点的充要条件:
 ,又
,又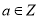 ,∴
,∴ 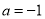 (Ⅲ)先化简不等式:
(Ⅲ)先化简不等式: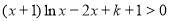 对任意的x∈
对任意的x∈ 恒成立,即
恒成立,即 ,令t(x)=
,令t(x)=  ,则
,则 ,
,
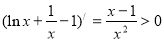 ,
, 在(1,+∞)上单调增,
在(1,+∞)上单调增,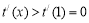
∴t(x) = 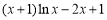 在(1,+∞)单调增,
在(1,+∞)单调增,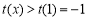 ,从而
,从而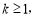 实数
实数 的最小值为1.
的最小值为1.
试题解析:【解析】
(Ⅰ)由题知 ------2分,
------2分, ∈(2,+∞)
∈(2,+∞)
(Ⅱ)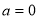 时,f(x)=-2x+1,零点为
时,f(x)=-2x+1,零点为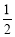 ,不合,舍去;
,不合,舍去;
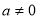 时,∵
时,∵  ∴
∴  ,
,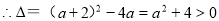 ,
,
∴函数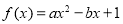 必有两个零点,
必有两个零点,
又函数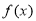 在
在 上恰有一个零点,∴
上恰有一个零点,∴
 ,又
,又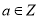 ,∴
,∴ 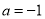
(Ⅲ)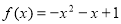 ,
, ,
, 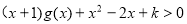 整理得
整理得
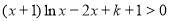
令H(x)= 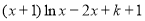 ,
,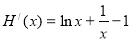 ,
,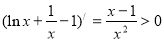
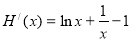 在(1,+∞)上单调增,又
在(1,+∞)上单调增,又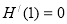 ,
,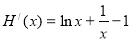 >0,
>0,
∴H(x) = 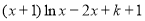 在(1,+∞)单调增,
在(1,+∞)单调增,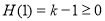 ,k≥1,k的最小值为1.----6分
,k≥1,k的最小值为1.----6分
考点:函数零点,不等式恒成立


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2014-2015学年江苏省等五校高三12月第一次联考文科数学试卷(解析版) 题型:解答题
函数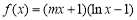 .
.
(1)若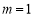 ,求曲线
,求曲线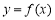 在
在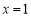 的切线方程;
的切线方程;
(2)若函数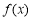 在
在 上是增函数,求实数
上是增函数,求实数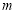 的取值范围;
的取值范围;
(3)设点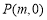 ,
,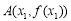 ,
,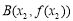 满足
满足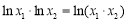
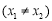 ,判断是否存在实数
,判断是否存在实数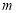 ,使得
,使得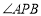 为直角?说明理由.
为直角?说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届江苏教育学院附属高中高三上学期期中理科数学试卷(解析版) 题型:解答题
(本题满分10分)已知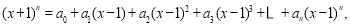 (其中
(其中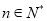 )
)
(1)求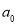 及
及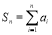 ;
;
(2)试比较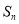 与
与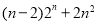 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届江苏教育学院附属高中高三上学期期中理科数学试卷(解析版) 题型:填空题
设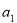 ,
,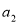 ,…,
,…,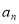 是各项不为零的
是各项不为零的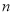 (
( )项等差数列,且公差
)项等差数列,且公差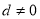 .若将此数列删去某一项后,得到的数列(按原来顺序)是等比数列,则所有数对
.若将此数列删去某一项后,得到的数列(按原来顺序)是等比数列,则所有数对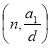 所组成的集合为____________.
所组成的集合为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com