
在下列命题中,
①“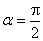 ”是“
”是“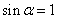 ”的充要条件;
”的充要条件;
② 的展开式中的常数项为
的展开式中的常数项为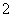 ;
;
③设随机变量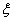 ~
~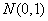 ,若
,若
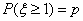 ,则
,则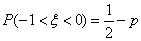 .
.
其中所有正确命题的序号是
A.② B.③
C.②③ D.①③
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:高中数学 来源: 题型:
以下判断正确的是( )
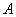 .函数
.函数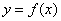 为
为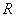 上的可导函数,则
上的可导函数,则 是
是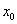 为函数
为函数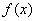 极值点的充要条件.
极值点的充要条件.
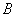 .命题“
.命题“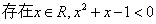 ”的否定是“
”的否定是“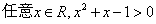 ”.
”.
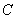 .命题“在
.命题“在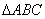 中,若
中,若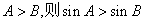 ”的逆
”的逆 命题为假命题.
命题为假命题.
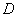 .“
.“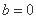 ”是“函数
”是“函数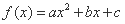 是偶函数”的充要条件.
是偶函数”的充要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆C: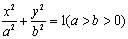 ,经过点
,经过点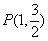 ,离心率
,离心率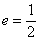 ,直线
,直线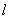 的方程为
的方程为 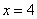 .
.
(1)求椭圆C的方程;
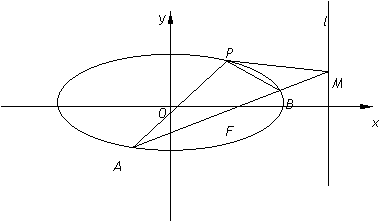 (2)AB是经过右焦点F的任一弦(不经过点P),设直线l与直线AB相交于点M,记PA、PB、PM的斜率分别为
(2)AB是经过右焦点F的任一弦(不经过点P),设直线l与直线AB相交于点M,记PA、PB、PM的斜率分别为 ,问:是否存在常数
,问:是否存在常数 ,使得
,使得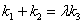 ?若存在,求出
?若存在,求出 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列 的各项均为正整数,且
的各项均为正整数,且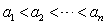 ,
,
设集合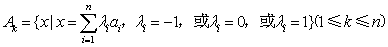 。
。
性质1 若对于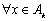 ,存在唯一一组
,存在唯一一组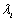 (
(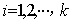 )使
)使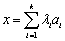 成立,则称数列
成立,则称数列 为完备数列,当k取最大值时称数列
为完备数列,当k取最大值时称数列 为k阶完备数列。
为k阶完备数列。
性质2 若记 ,且对于任意
,且对于任意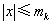 ,
,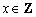 ,都有
,都有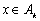 成立,则称数列
成立,则称数列 为完整数列,当k取最大值时称数列
为完整数列,当k取最大值时称数列 为k阶完整数列。
为k阶完整数列。
性质3 若数列 同时具有性质1及性质2,则称此数列
同时具有性质1及性质2,则称此数列 为完美数列,当
为完美数列,当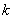 取最大值时
取最大值时 称为
称为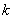 阶完美数列;
阶完美数列;
(Ⅰ)若数列 的通项公式为
的通项公式为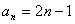 ,求集合
,求集合 ,并指出
,并指出 分别为几阶完备数列,几阶完整数列,几阶完美数列;
分别为几阶完备数列,几阶完整数列,几阶完美数列;
(Ⅱ)若数列 的通项公式为
的通项公式为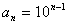 ,求证:数列
,求证:数列 为
为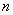 阶完备数列,并求出集合
阶完备数列,并求出集合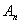 中所有元素的和
中所有元素的和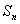 。
。
(Ⅲ)若数列 为
为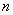 阶完美数列,求数列
阶完美数列,求数列 的通项公式。
的通项公式。
查看答案和解析>>
科目:高中数学 来源: 题型:
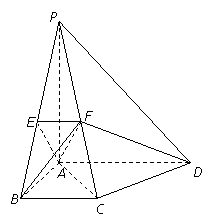
如图,在四棱锥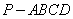 中,平面
中,平面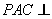 平面
平面 ,且
,且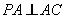 ,
, 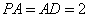 .四边形
.四边形 满足
满足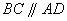 ,
,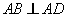 ,
,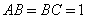 .点
.点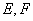 分别为侧棱
分别为侧棱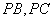 上的点,且
上的点,且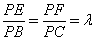 .
.
(Ⅰ)求证: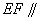 平面
平面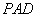 ;
;
(Ⅱ)当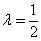 时,求异面直线
时,求异面直线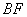 与
与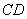 所成角的余弦值;
所成角的余弦值;
(Ⅲ)是否存在实数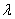 ,使得平面
,使得平面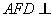 平面
平面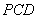 ?若存在,试求出
?若存在,试求出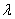 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com