
已知数列 的各项均为正整数,且
的各项均为正整数,且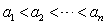 ,
,
设集合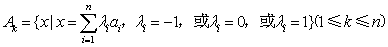 。
。
性质1 若对于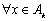 ,存在唯一一组
,存在唯一一组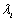 (
(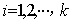 )使
)使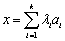 成立,则称数列
成立,则称数列 为完备数列,当k取最大值时称数列
为完备数列,当k取最大值时称数列 为k阶完备数列。
为k阶完备数列。
性质2 若记 ,且对于任意
,且对于任意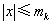 ,
,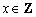 ,都有
,都有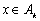 成立,则称数列
成立,则称数列 为完整数列,当k取最大值时称数列
为完整数列,当k取最大值时称数列 为k阶完整数列。
为k阶完整数列。
性质3 若数列 同时具有性质1及性质2,则称此数列
同时具有性质1及性质2,则称此数列 为完美数列,当
为完美数列,当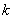 取最大值时
取最大值时 称为
称为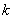 阶完美数列;
阶完美数列;
(Ⅰ)若数列 的通项公式为
的通项公式为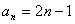 ,求集合
,求集合 ,并指出
,并指出 分别为几阶完备数列,几阶完整数列,几阶完美数列;
分别为几阶完备数列,几阶完整数列,几阶完美数列;
(Ⅱ)若数列 的通项公式为
的通项公式为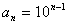 ,求证:数列
,求证:数列 为
为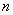 阶完备数列,并求出集合
阶完备数列,并求出集合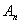 中所有元素的和
中所有元素的和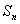 。
。
(Ⅲ)若数列 为
为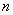 阶完美数列,求数列
阶完美数列,求数列 的通项公式。
的通项公式。
解:(Ⅰ)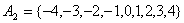 ;
;
 为2阶完备数列,
为2阶完备数列,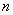 阶完整数列,2阶完美数列;
阶完整数列,2阶完美数列;
(Ⅱ)若对于
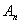 ,假设存在2组
,假设存在2组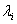 及
及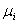 (
(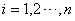 )使
)使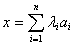 成立,则有
成立,则有
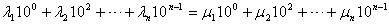 ,即
,即
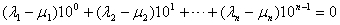 ,其中
,其中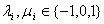 ,
,
必有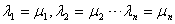 ,
,
所以仅存在唯一一组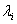 (
(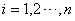 )使
)使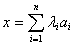 成立,
成立,
即数列 为
为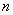 阶完备数列;
阶完备数列;
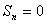 ,对
,对
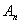 ,
,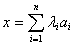 ,则
,则 ,因为
,因为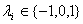 ,则
,则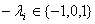 ,所以
,所以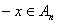 ,即
,即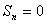
(Ⅲ)若存在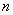 阶完美数列,则由性质1易知
阶完美数列,则由性质1易知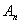 中必有
中必有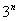 个元素,由(Ⅱ)知
个元素,由(Ⅱ)知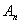 中元素成对出现(互为相反数),且
中元素成对出现(互为相反数),且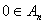 ,又
,又 具有性质2,则
具有性质2,则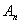 中
中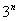 个元素必为
个元素必为
 ,
,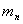
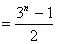 。
。
下面用数学归纳法证明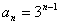
显然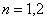 时命题成立,假设当
时命题成立,假设当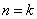 (
(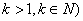 时命题成立,即
时命题成立,即
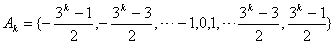
当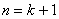 时,只需证
时,只需证
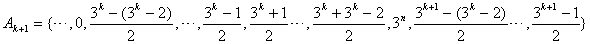 由于对称性只写出了
由于对称性只写出了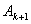 元素正的部分,其中
元素正的部分,其中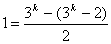
既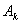 中正的部分的
中正的部分的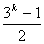 个元素统一为
个元素统一为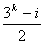 ,其中
,其中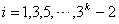
则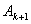 中从
中从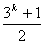 ,到
,到 这
这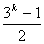 个元素可以用
个元素可以用 唯一表示其中
唯一表示其中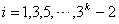 ,
,
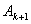 中从(
中从(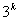 +1)到最大值
+1)到最大值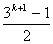 这
这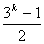 个元素可用
个元素可用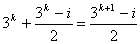 唯一表示
唯一表示
其中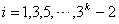
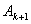 中正的部分
中正的部分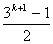 个元素都存在唯一一组
个元素都存在唯一一组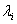 (
(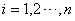 )使
)使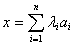 成立,
成立,
所以当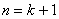 时命题成立。
时命题成立。
即{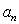 }为
}为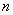 阶完美数列,
阶完美数列,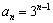


科目:高中数学 来源: 题型:
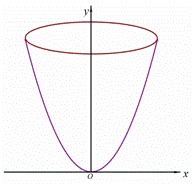
抛物线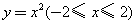 绕
绕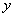 轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的体积是
轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的体积是
(A)1 (B)8 (C)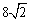 (D)
(D)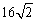
查看答案和解析>>
科目:高中数学 来源: 题型:
在下列命题中,
①“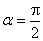 ”是“
”是“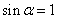 ”的充要条件;
”的充要条件;
② 的展开式中的常数项为
的展开式中的常数项为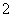 ;
;
③设随机变量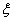 ~
~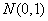 ,若
,若
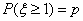 ,则
,则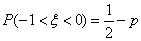 .
.
其中所有正确命题的序号是
A.② B.③
C.②③ D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
在一次抽奖活动中,有a、b、c、d、e、f 共6人获得抽奖的机会。抽奖规则如下:主办方先从6人中随机抽取两人均获一等奖,再从余下的4人中随机抽取1人获二等奖,最后还从这4人中随机抽取1人获三等奖。
(Ⅰ)求a能获一等奖的概率;
(Ⅱ)若a、b已获一等奖,求c能获奖的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com