
 =(k,1),
=(k,1), =(2,4),若|
=(2,4),若| |≤4,则△ABC是直角三角形的概率是________.
|≤4,则△ABC是直角三角形的概率是________.
 =(k,1),|
=(k,1),| |≤4由公式展开,根据k∈Z确定出向量的个数,然后求出向量
|≤4由公式展开,根据k∈Z确定出向量的个数,然后求出向量 的坐标,对三个角为直角的情况进行讨论,求出参数的可能取值,再计算概率
的坐标,对三个角为直角的情况进行讨论,求出参数的可能取值,再计算概率 =(k,1),|
=(k,1),| |≤4,
|≤4, =(2,4),故向量
=(2,4),故向量 =(2-k,3),
=(2-k,3),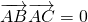 ,得2k+4=0解得k=-2符合题意,
,得2k+4=0解得k=-2符合题意, =0得2k-k2+3=0,解得k=-3,或k=1,符合题意,
=0得2k-k2+3=0,解得k=-3,或k=1,符合题意, =0,得4-2k+12=0解得k=8,不符合题意故舍,
=0,得4-2k+12=0解得k=8,不符合题意故舍, ;
; .
.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com